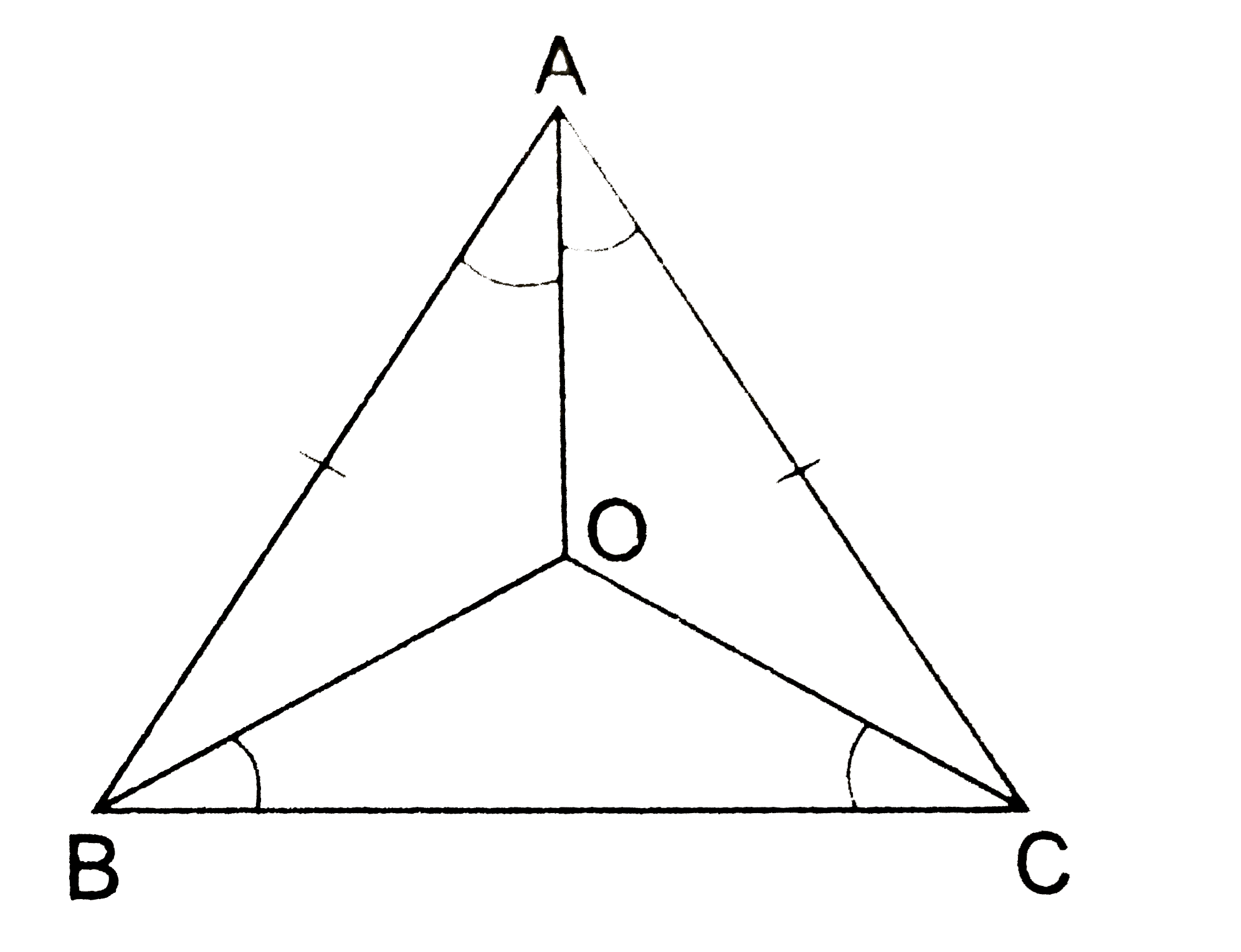
In $Δ A B C$ , bisectors of $∠ B and ∠ C$ interesct each other at point O. Prove that $∠ B O C = 90^{\circ} + \frac{1}{2} ∠ A i . e ., ∠ 1 = 90^{\circ} + \frac{1}{2}$

Video Solution

Text Solution

Verified by Experts

In $Δ O B C$ ,
$∠ 1 + ∠ 3 + ∠ 4 = 180^{\circ}$ (angle sum property )....(1)
In $Δ A B C$ ,
$∠ A + ∠ B ∠ C = 180^{\circ}$ (angle sum property)

$\Rightarrow \frac{1}{2} ∠ A + \frac{1}{2} ∠ B + \frac{1}{2} ∠ C = 90^{\circ}$
$\Rightarrow \frac{1}{2} ∠ A + ∠ 4 = 90^{\circ}$ ( $∴ B o and C O$ are bisectores of $∠ B and ∠ C$ )
$\Rightarrow \frac{1}{2} ∠ + 180^{\circ} - ∠ 1 = 90^{\circ}$ [from (1)]
$\Rightarrow ∠ 1 = 180^{\circ} - 90^{\circ} + \frac{1}{2} ∠ A$
$\Rightarrow ∠ 1 = 90^{\circ} + \frac{1}{2}$

In a $Δ A B C,$ the bisectors of $∠ B and ∠ C$ intersect each other point O. Then $∠ B O C$ is ?
A $∠ B O C = 180^{\circ} + \frac{1}{2} ∠ A$ .
B $∠ B O C = 90^{\circ} + \frac{1}{2} ∠ A$ .
C $∠ B O C = 180^{\circ} - \frac{1}{2} ∠ A$ .
D $∠ B O C = 90^{\circ} - \frac{1}{2} ∠ A$ .
In $△ A B C$ the bisectors of $∠ B$ and $∠ C$ intersect at I if $∠ A = 70^{\circ}$ then $∠ B I C = \dots \dots \dots \dots . .$
A $35^{\circ}$
B $75^{\circ}$
C $100^{\circ}$
D $125^{\circ}$