In ΔABC,AB=AC and the bisectors of ∠Band∠C meet at a point O. Prove that BO = CO and the ray AO is the bisector of ∠A.
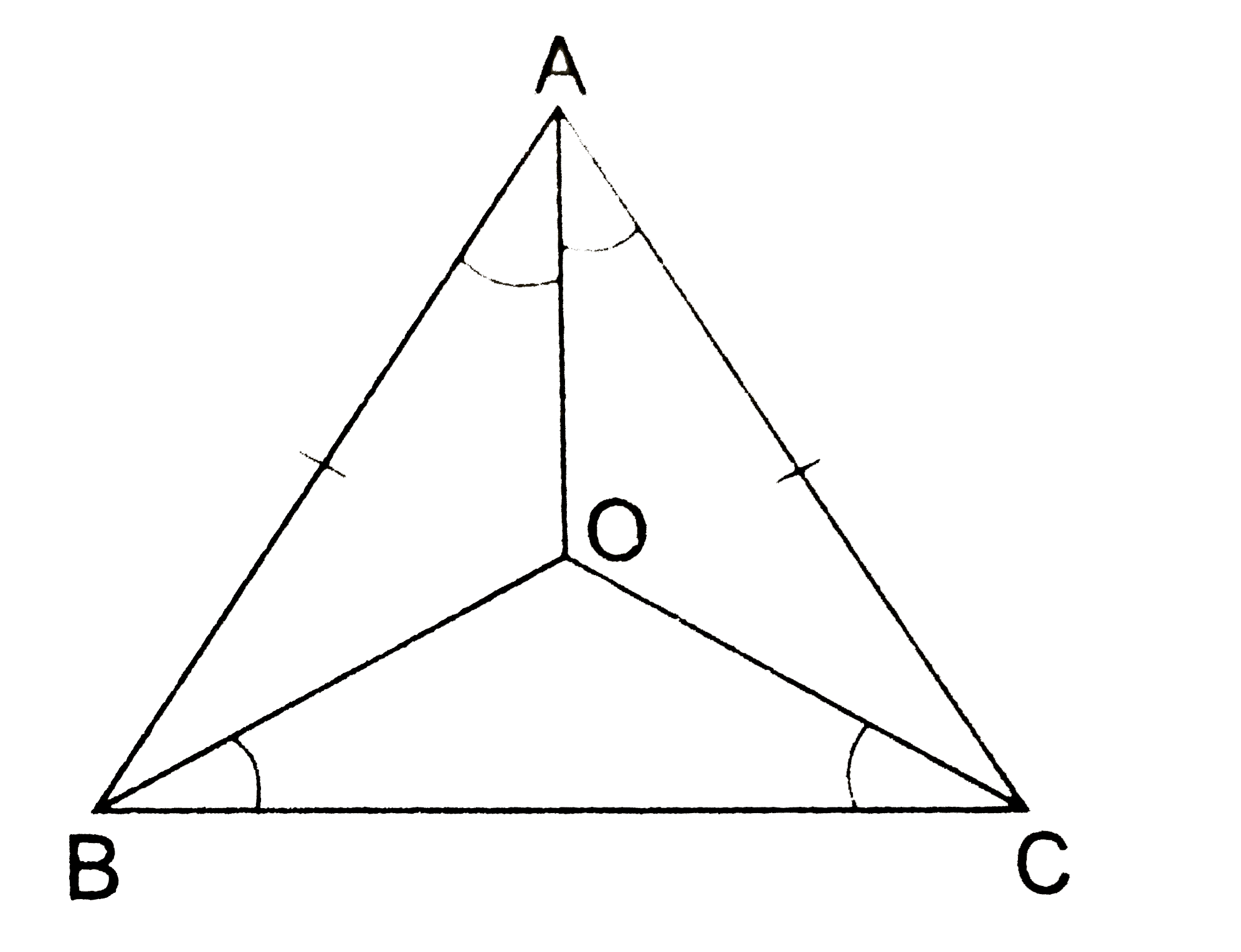
AB=AC⇒∠B=∠C⇒12∠B=12∠C⇒∠OBC=∠OCB⇒BO=CO.
Now, ΔAOB≅ΔAOC as AB=AC,BO=CO,AO=AO.
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Multiple Choice Questions (Mcq)
20 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
In ΔABC,AB=AC and the bisectors of ∠B and ∠C meet at a point O. Prove that BO=CO and the ray AO is the bisector of ∠A.
View SolutionIn ABC, AB=AC, and the bisectors of angles B and C intersect at point O. Prove that BO=CO and the ray AO is the bisector of angle BAC
Since the angles opposite to equal sides are equal,
AB=AC
⇒∠C=∠B
⇒2∠B=2∠C
Since BO and CO are bisectors of ∠Band∠C, we also have
∠ABO=2∠B
∠ACO=2∠C
∠ABO=2∠B=2∠C=∠ACO.
Consider △BCO:∠OBC=∠OCB
BO=CO(Sides opposite to equal angles are equal)
Finally, consider triangles ABO and ACO.
BA=CA(given)
BO=CO(proved)
∠ABO=∠ACO (proved)
Hence, by S.A.S postulate△ABO≅△ACO
∠BAO=∠CAO
AObisects∠A.
View Solution
Knowledge Check
In a ΔABC, the bisectors of ∠Band∠C meet at point O within the triangle. If ∠A=132∘ then the measure of ∠BOC is(in degrees) :
A166∘B84∘C156∘D120∘
In ABC,AB=AC, and the bisectors of angles B and C intersect at point O . Prove that BO=CO and the ray AO is the bisector of angles BAC.
View SolutionIn ΔABC,AB=AC and the bisectors of ∠B and ∠C meet AC and AB at point D and E respectively. Prove that BD=CE.
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View SolutionTriangle ABC is an isosceles triangle with AB=AC. Bisectors of ∠Band∠C intersect each other at O. join A−O and prove that
AO is bisector of ∠A
View SolutionIn △ABC,∠A=40∘ if bisector of ∠B and ∠C meets at O then prove that ∠BOC=110∘
View SolutionIn ΔABC exterior angle bisectors of ∠Band∠C meets at point P if ∠BAC=80∘ then find ∠BPC.
View SolutionIn a parallelogram ABCD, the bisectors of ∠Aand∠B intersect each other at point P. Prove that ∠APB=90∘.
View Solution
