In ΔABC it is given that D is the midpoint of BC, E is the midpoint of BD and O is the midpoint of AE . Then, find ar (ΔBOE) .
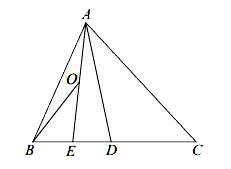
13ar(ΔABC)
14ar(ΔABC)
16ar(ΔABC)
18ar(ΔABC)
The correct Answer is:D
Step by step video, text & image solution for In DeltaABC it is given that D is the midpoint of BC, E is the midpoint of BD and O is the midpoint of AE . Then, find ar (Delta BOE) . by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Topper's Solved these Questions
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - Everyday mathematics10videos
IMO QUESTION PAPER 2016 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET BEXERCISE - Achievers section5videos
IMO QUESTION PAPER 2016 SET B
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2016 SET A EXERCISE - Achievers Section5videos
IMO QUESTION PAPER 2016 SET A
- BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2017 SET BEXERCISE - ACHIEVERS SECTION5videos
IMO QUESTION PAPER 2017 SET B
Similar Questions
Knowledge Check
- Question 1 - Select One
In △ABC, if D is the midpoint of BC and E is the midpoint of AD then ar(△BED) = ?
 A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC)
A12ar(△ABC)B13ar(△ABC)C14ar(△ABC)D23ar(△ABC) - Question 2 - Select One
In triangle ABC,D is the midpoint of AB, E is the midpoint of DB and F is the midpoint of BC. If the area of ΔABC is 96, the area of ΔAEF is
A16B24C32D36 - Question 3 - Select One
The area of ΔABC is 44 cm2 . If D is the midpoint of BC and E is the midpoint of AB, then the area ( in cm2) of ΔBDE is :
A5.5B22C11D44
In the given figure. AB∣CDandO is the midpoint of AD.
View SolutionD is the mid-point of side BC of ΔABC and E is the mid-point of BO. If O is the mid-point of AE, then ar(ΔBOE) = 1/k ar(ΔABC). Then k equals
View SolutionIn ΔABC, D is the midpoint of side BC, E is mid point of AD, F is midpoint of BE and G is mid-point of FC. What part of the area of ΔABC is the area of ΔEFG?
View SolutionABC is a triangle in which D is the midpoint of BC and E is the midpoint of AD.
Prove that ar(△BED)=14ar(△ABC).
 View Solution
View SolutionIn ΔABC, P is a point on BC such that BP : PC = 2 : 3 and Q is the midpoint of BP. Then ar (ΔABQ):ar(ΔABC) is equal to :
View Solution



