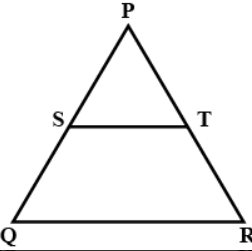
In and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT.
Step by step video, text & image solution for In DeltaPQR,Pq=PR and S is the mid-point of PQ. A line drawn from S parallel to QR, intersects the line PR at T. Prove that PS = PT. by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (very Short Answer Questions)
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Revision Exercise (short Answer Questions )
10 Videos
- QUADRILATERALSBOOK - NAGEEN PRAKASHANCHAPTER - QUADRILATERALSEXERCISE - Exercise 8a
29 Videos
- PROBABILITYBOOK - NAGEEN PRAKASHANCHAPTER - PROBABILITYEXERCISE - Revision Exercise (very Short Answer /short Answer Questions)
10 Videos
- STATISTICSBOOK - NAGEEN PRAKASHANCHAPTER - STATISTICSEXERCISE - Revision Exercise
10 Videos
Similar Questions
PQR is a triangle is which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT
In△PQR,wehavePQ=PR
View SolutionIn figure, PQR is a triangle in which PQ=PR and S is any point on the side PQ . Through S, a line is drawn parallel to QR and intersecting PR at T. Prove that PS=PT.
View Solution
Knowledge Check
In ΔPQR, QR=10, RP=11 and PQ=12. D is the midpoint of PR, DE is drawn parallel to PQ meeting QR in E. EF is drawn parallel to RP meeting PQ in F. What is the length of DF?
A112B6C334D5If S is the midpoint of a straight line PQ and R is a point different from S , such that PR = RQ , then
A∠PRS=90∘B∠QRS=90∘C∠PSR=90∘D∠QSR<90∘
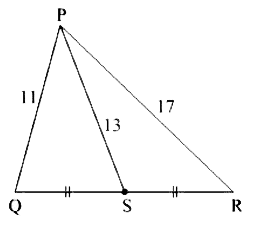
In ΔPQR, point S is the midpoint of side QR. If PQ =11, PR =17 PS =13 , find QR.
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View SolutionIn ΔPQR, point S is the midoint of side QR. If PQ=11,PR=17,PS=13, Find QR.
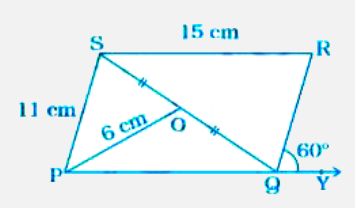
View SolutionIn parallelogram PQRS, O is the mid point of SQ. Find ∠S, ∠R, PQ, QR and diagonal PR.
View SolutionIf S is the midpoint of a straight line PQ and R is a point different from S, such that PR = RQ then
View SolutionIf Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
View Solution
