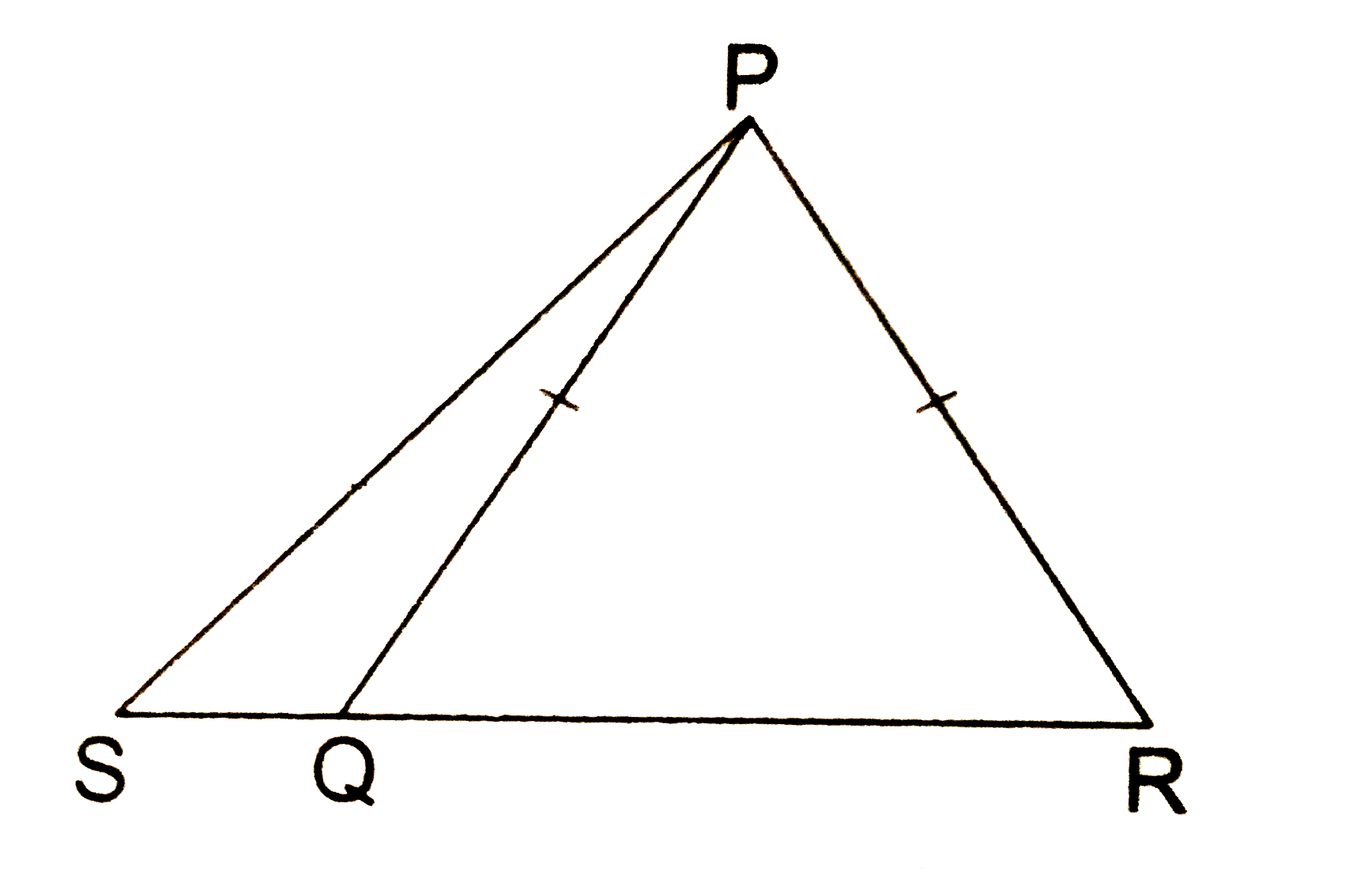
If Q is a point on the side SR of a triangle PSR such that PQ=PR then prove that PS>PQ
To prove that PS>PQ given that PQ=PR in triangle PSR where Q is a point on side SR, we can follow these steps:
Step 1: Identify the Angles
Let’s label the angles in triangle PSR and triangle PQR:
- Let ∠PQR=∠1
- Let ∠PRQ=∠2
- Let ∠QRP=∠3
- Let ∠PSQ=∠4
- Let ∠PQR=∠5
- Let ∠QPS=∠6
Step 2: Use the Exterior Angle Theorem
Since ∠2 is an exterior angle for triangle PQR, we can express it as:
∠2=∠5+∠6
Step 3: Apply the Exterior Angle Theorem Again
Now, ∠4 is an exterior angle for triangle PSQ, so we can express it as:
∠4=∠1+∠3
Step 4: Use the Given Condition
Since PQ=PR, by the Isosceles Triangle Theorem, we know that:
∠2=∠5
This means that the angles opposite to equal sides are equal.
Step 5: Substitute the Angles
Now we can substitute ∠5 in the equation for ∠2:
∠2=∠1+∠3
Step 6: Combine the Equations
Now we have:
∠2=∠5+∠6
Substituting ∠5 from the previous step:
∠5+∠6=∠1+∠3
Step 7: Analyze the Angles
From the above equation, we can see that:
∠6>∠1
This implies that:
∠2>∠1
Step 8: Relate the Angles to the Sides
By the property of triangles, if an angle is greater, the side opposite to it is also greater. Hence:
PS>PQ
Conclusion
Thus, we have proved that PS>PQ.
---
Let’s label the angles in triangle PSR and triangle PQR:
- Let ∠PQR=∠1
- Let ∠PRQ=∠2
- Let ∠QRP=∠3
- Let ∠PSQ=∠4
- Let ∠PQR=∠5
- Let ∠QPS=∠6
Since ∠2 is an exterior angle for triangle PQR, we can express it as:
∠2=∠5+∠6
Now, ∠4 is an exterior angle for triangle PSQ, so we can express it as:
∠4=∠1+∠3
Since PQ=PR, by the Isosceles Triangle Theorem, we know that:
∠2=∠5
This means that the angles opposite to equal sides are equal.
Now we can substitute ∠5 in the equation for ∠2:
∠2=∠1+∠3
Now we have:
∠2=∠5+∠6
Substituting ∠5 from the previous step:
∠5+∠6=∠1+∠3
From the above equation, we can see that:
∠6>∠1
This implies that:
∠2>∠1
By the property of triangles, if an angle is greater, the side opposite to it is also greater. Hence:
PS>PQ
Thus, we have proved that PS>PQ.
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
If S is a point on side PQ of a ΔPQR such that PS=QS=RS, then
APR⋅QR=RS2BQS2+RS2=QR2CPR2+QR2=PQ2DPS2+RS2=PR2 - Question 2 - Select One
S and U are two points on the side PQ of ΔPQR , such that QU=PS . If ST||QR and UV∣∣PR , then
ATV||PQBTV⊥PQCTV and PQ intersect at 60∘DTV and PQ intersect at 45∘
S is any point in the interior of a △PQR . Prove that SQ+SR<PQ+PR
View SolutionS in any point on side QR of a ΔPQR.ShowtˆPQ + QR+RP gt 2PS.
View Solution∠PQR=∠PRS, then prove that ∠PQS=∠PRT
View SolutionIn Figure, T is a point on side QR of PQR and S is a point such that RT=ST. Prove That : PQ+PR>QS
 View Solution
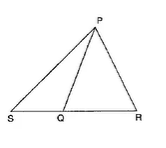
View SolutionIn Figure, PQ=PR. Show that PS>PQ
 View Solution
View SolutionIf S is the mid-point of side QR of a ΔPQR, then prove that PQ+PR=2PS.
View Solution