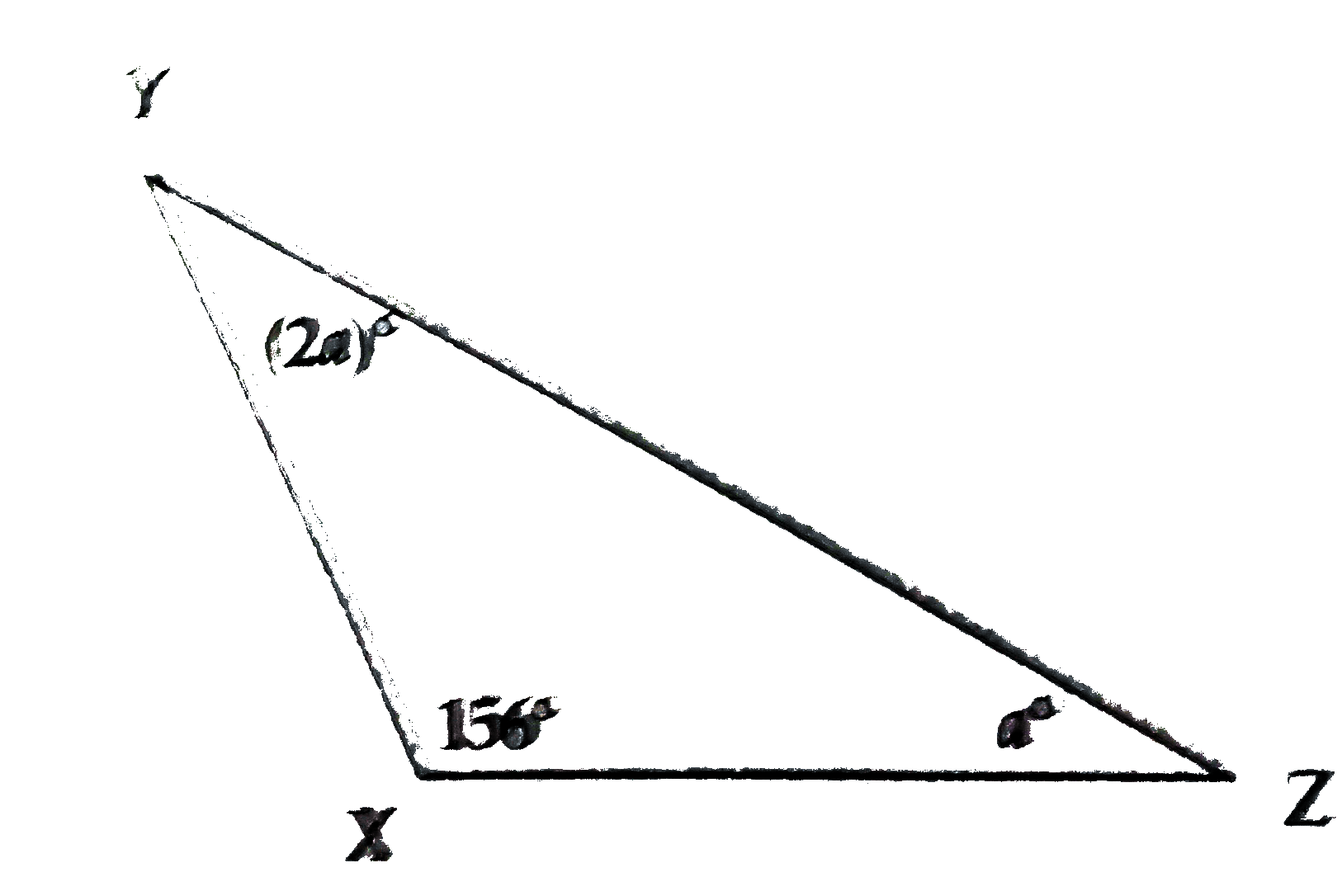
In ΔXYZ,XA is the altidue from X on YZ. Show that XY+YZ+ZX>2XA.
To prove that XY+YZ+ZX>2XA in triangle ΔXYZ where XA is the altitude from point X to side YZ, we can follow these steps:
Step 1: Understand the Triangle and the Altitude
We start with triangle XYZ and draw the altitude XA from point X to side YZ. This creates two right triangles: ΔXYA and ΔXZA.
Step 2: Apply the Triangle Inequality
We will use the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
1. For triangle XYA:
XY+YA>XA(Equation 1)
2. For triangle XZA:
XZ+ZA>XA(Equation 2)
Step 3: Express YZ in terms of YA and ZA
Since A is the foot of the altitude from X to YZ, we can express YZ as:
YZ=YA+AZ(Equation 3)
Step 4: Add the Inequalities
Now, we will add the inequalities from Equation 1 and Equation 2:
(XY+YA)+(XZ+ZA)>XA+XA
This simplifies to:
XY+XZ+YA+ZA>2XA
Step 5: Substitute YA+ZA with YZ
From Equation 3, we can substitute YA+ZA with YZ:
XY+XZ+YZ>2XA
Conclusion
Thus, we have shown that:
XY+YZ+ZX>2XA
We start with triangle XYZ and draw the altitude XA from point X to side YZ. This creates two right triangles: ΔXYA and ΔXZA.
We will use the triangle inequality theorem, which states that the sum of the lengths of any two sides of a triangle is greater than the length of the third side.
XY+YA>XA(Equation 1)
XZ+ZA>XA(Equation 2)
Since A is the foot of the altitude from X to YZ, we can express YZ as:
YZ=YA+AZ(Equation 3)
Now, we will add the inequalities from Equation 1 and Equation 2:
(XY+YA)+(XZ+ZA)>XA+XA
This simplifies to:
XY+XZ+YA+ZA>2XA
From Equation 3, we can substitute YA+ZA with YZ:
XY+XZ+YZ>2XA
Thus, we have shown that:
XY+YZ+ZX>2XA
Topper's Solved these Questions
- THE TRIANGLE AND ITS PROPERTIESBOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - CHALLENGE
1 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - REVISIONS EXERCISE
15 Videos
- THE TRIANGLE AND ITS PROPERTIESBOOK - ICSECHAPTER - THE TRIANGLE AND ITS PROPERTIESEXERCISE - EXERCISE 12.2
11 Videos
- SYMMETRYBOOK - ICSECHAPTER - SYMMETRYEXERCISE - Exercise 19B
13 Videos
- UNITARY METHODBOOK - ICSECHAPTER - UNITARY METHODEXERCISE - EXERCISE
16 Videos
Similar Questions
Knowledge Check
If 8x−8yz+2=74. What is the value of x-yz?
A2B6C9D16
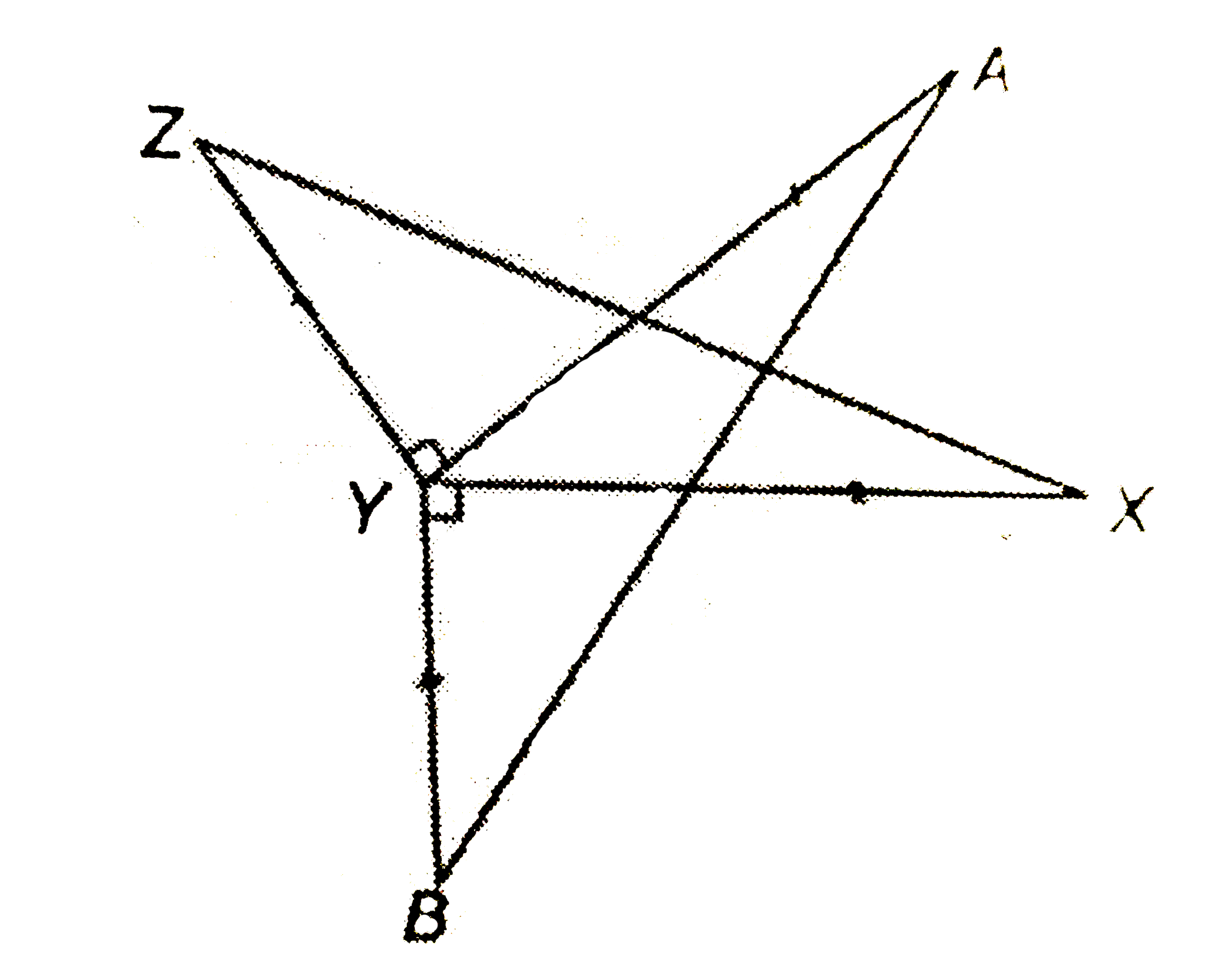
In the adjoining figure, ∠AYZ=∠BYX=90∘,AY=YZ and XY=BY. Prove that AB=ZX.
View SolutionIf y is the mean proportional between x and z, show that xy+yz is the mean proportional between x^(2) + y^(2) and y^(2) + z^(2).
View SolutionDraw a line segment XY = 7 cm. Take a point A on it such that XA = 4cm. Draw a perpendicular to XY through the point A.
View SolutionThe intersection of XY-plane and YZ-plane is known as
View SolutionUsing the properties of determinants, show that:
⎡⎢⎣xx2yzyy2zxzz2xy⎤⎥⎦=(x−y)(y−z)(z−x)(xy+yz+zx)
View SolutionAxy,yz,Azx be the area of projections oif asn area a o the xy,yz and zx and planes resepctively, then A2=A2_(xy)+A2_(yz)+a2_(zx)
View SolutionThe shorteast distance from (1,1,1) to the line of intersection of the pair of planes xy+yz+zx+y2=0 is
View Solution