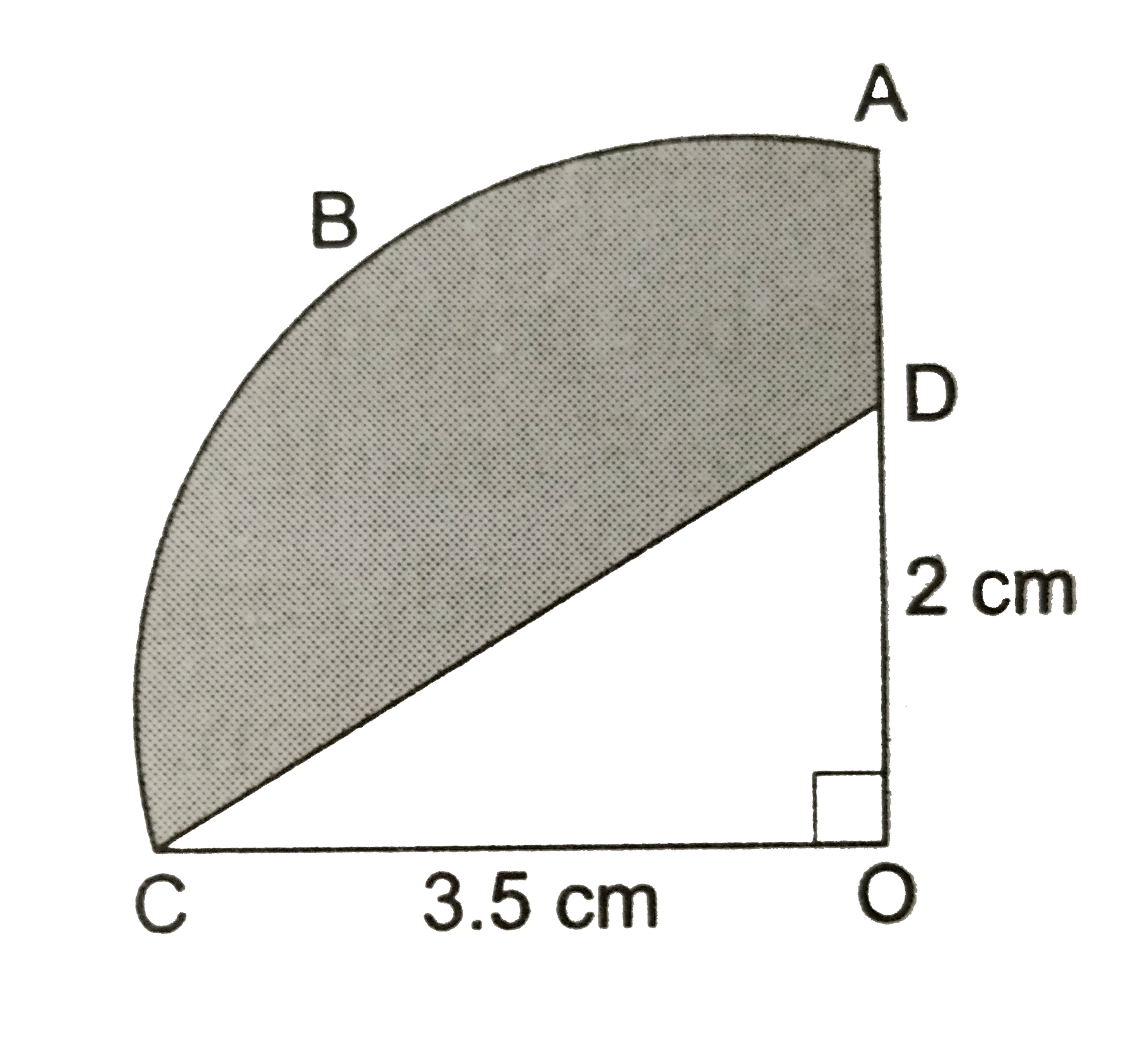
In Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2cm, find the area of the
(i) quadrant OACB, (ii) shaded region.
Area of quadrant OACB, can be give as , A=θ360∗πr2
Here, θ=∠AOB=90∘andr=OB+OA=2cm
So, A=90360∗227∗3.5∗3.5=14∗11∗3.5
A=38.54=9.625cm2
Now, Area of Shaded region,AS= Area of OACB - Area of ΔOBD
Area of ΔOBD=12∗OB∗OD=12∗3.5∗2=3.5cm2
So, area of shaded region, AS=9.625−3.5=6.125cm2
Similar Questions
In Fig. 12.30, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2cm, find the area of the
(i) quadrant OACB, (ii) shaded region.View SolutionIn Fig. 15.70, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2 cm , find the area of the (i) quadrant OACB (ii) shaded region. (FIGURE)
View SolutionIn the given figwe, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD = 2 cm, find the area of the
(i) quadrant OACB,
(ii) shaded region.
 View Solution
View SolutionIn figure, OACB is a quadrant of a circle with centre O and radius 7 cm. If AD = 2 cm, find the area of the shaded region.
 View Solution
View SolutionIn the given figure OABC is a quadrant of a circle with centre O and radius 3.5cm.If OD=2cm,find the area of the shaded region.
 View Solution
View SolutionOACB is a quadrant of a circle with centre O and its radius is 3.5cm . If OD=2cm, find the area of the shaded region. [Take π=227]
 View Solution
View SolutionIn the given Fig. 12.30, find the area of the shaded region.
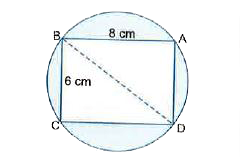 View Solution
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn Fig. 12.55, AB and CD are two perpendicular diameters of a circle with centre O. If OA= 7 cm, find the area of the shaded region. (Use π=227).
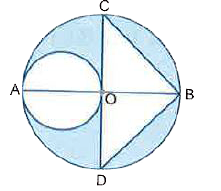 View Solution
View SolutionIn the given figure, two concentric circles with centre O have radii 21 cm and 42 cm. If ∠AOB=60∘ find the area of the shaded region.
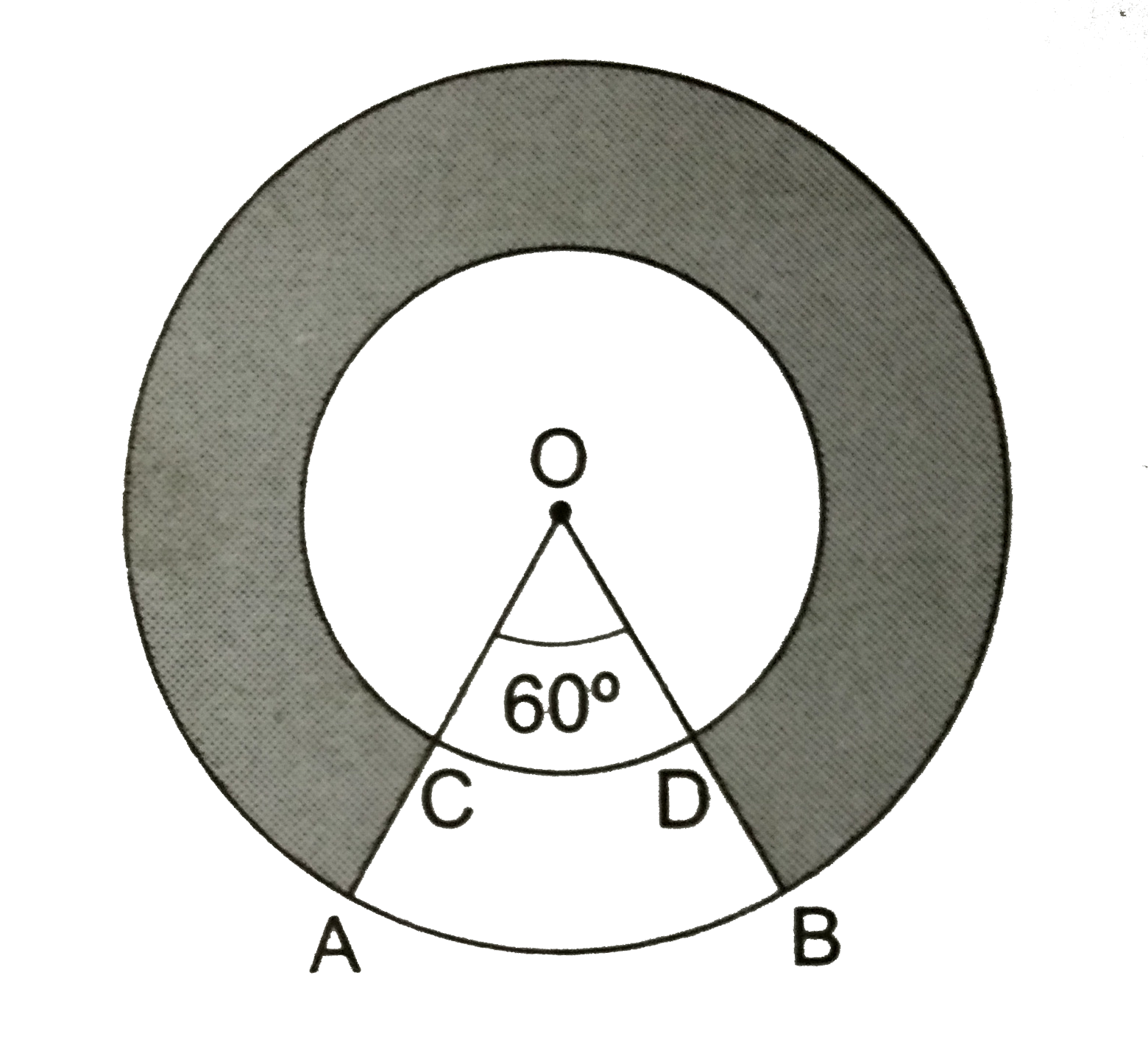 View Solution
View Solution

