In Fig. 15.35, AOBCA represents a quadrant of a circle of radius 3.5 cm with centre O . Calculate the area of the shaded portion (Take π=22/7) .
To find the area of the shaded portion in the quadrant of a circle with radius 3.5 cm, we will follow these steps:
Step 1: Calculate the area of the quadrant
The area of a quadrant (which is a quarter of a circle) can be calculated using the formula:
Area of Quadrant=θ360×πr2
Here, θ=90∘ for a quadrant, and r=3.5cm.
Substituting the values:
Area of Quadrant=90360×227×(3.5)2
Calculating (3.5)2:
(3.5)2=12.25
Now substituting this back into the area formula:
Area of Quadrant=14×227×12.25
=22×12.2528
=271.528≈9.67857cm2
Step 2: Calculate the area of the triangle
The area of the triangle formed in the quadrant can be calculated using the formula:
Area of Triangle=12×base×height
In this case, the base and height of the triangle are both equal to the radius of the circle, which is 3.5cm.
Substituting the values:
Area of Triangle=12×3.5×3.5
=12×12.25=6.125cm2
Step 3: Calculate the area of the shaded portion
Now, we can find the area of the shaded portion by subtracting the area of the triangle from the area of the quadrant:
Area of Shaded Portion=Area of Quadrant−Area of Triangle
=9.67857−6.125
≈3.55357cm2
Final Answer
The area of the shaded portion is approximately 3.55cm2.
---
The area of a quadrant (which is a quarter of a circle) can be calculated using the formula:
Area of Quadrant=θ360×πr2
Here, θ=90∘ for a quadrant, and r=3.5cm.
Area of Quadrant=90360×227×(3.5)2
(3.5)2=12.25
Area of Quadrant=14×227×12.25
=22×12.2528
=271.528≈9.67857cm2
The area of the triangle formed in the quadrant can be calculated using the formula:
Area of Triangle=12×base×height
In this case, the base and height of the triangle are both equal to the radius of the circle, which is 3.5cm.
Area of Triangle=12×3.5×3.5
=12×12.25=6.125cm2
Now, we can find the area of the shaded portion by subtracting the area of the triangle from the area of the quadrant:
Area of Shaded Portion=Area of Quadrant−Area of Triangle
=9.67857−6.125
≈3.55357cm2
The area of the shaded portion is approximately 3.55cm2.
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the figure given below, ABCO represents a quadrant of a circle of radius 10.5 cm with centre O. Calculate the area of shaded portion, if OD = DC.
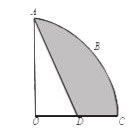 A59.06cm2B69cm2C79cm2D49cm2
A59.06cm2B69cm2C79cm2D49cm2
ABCP is a quadrant of a circle of radius 14 cm. with AC as diameter, a semicircle is drawn. Find the area of the shaded portion
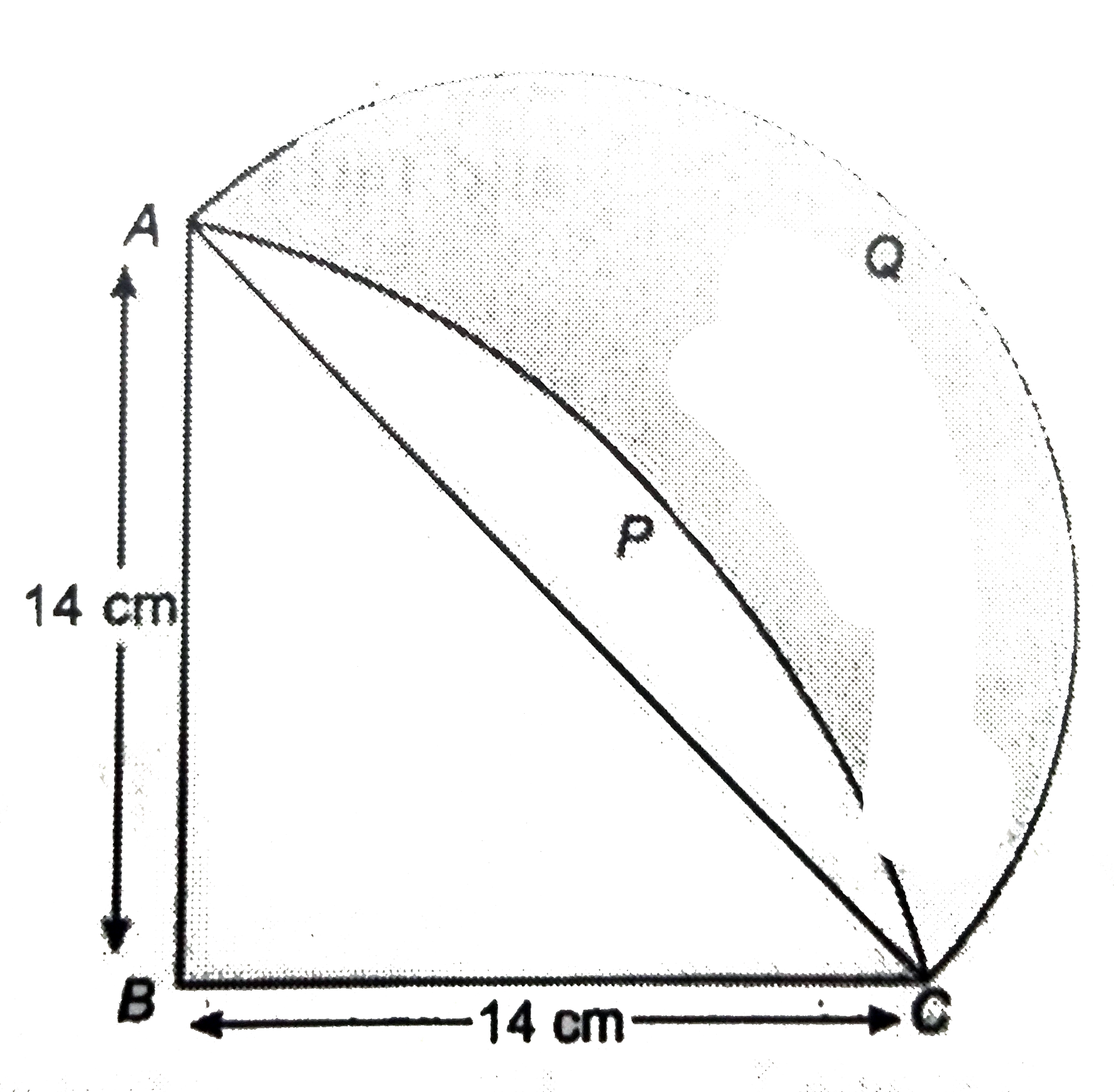
View SolutionIn Fig. 19.60, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O . Find the area of the shaded region. (FIGURE)
View SolutionIn Fig. 12.64, ABCP is a quadrant of a circle of radius 20 cm. With AC as diameter, a semi-cirde is drawn. Find the area of the shaded portion.

View SolutionABCP is a quadrant of a circle of radius 14 cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionBCP is a quadrant of a circle of radius 14cm. With AC as diameter, a semi-circle is drawn. Find the area of the shaded portion.
View SolutionIn Fig. 15.72 (a) , OABC is a square of side 7 cm. If OAPC is a quadrant of a circle with centre O , then find the area of the shaded region. (Use π=22/7) (FIGURE)
View SolutionIn the given figure, ABC is an equilateral triangle inscribed in a circle of radius 4 cm with centre O, then the area of the shaded region is :
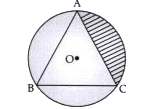
View Solution

