In Fig. 15.92, two circles with centres A and B touch each other at the point C . If AC=8 cm and AB=3 cm , find the area of the shaded region. (FIGURE)
Step by step video & image solution for In Fig. 15.92, two circles with centres A and B touch each other at the point C . If A C=8\ c m and A B=3\ c m , find the area of the shaded region. (FIGURE) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Three circles with centres A, B and C and with unit radii touch each other at O, P and Q. Find the area of the shaded region .
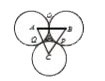 A0.16 sq. unitsB1.21 sq. unitsC0.03 sq. unitsD0.32 units
A0.16 sq. unitsB1.21 sq. unitsC0.03 sq. unitsD0.32 unitsABCD is a square . A circle is inscribed in the square . Also taking A,B,C,D ( the vertices of squares ) as the centres of four quadrants , drawn inside the circel , which are touching each other on the mid-points of the sides of square . Area of square is 4cm2. What is the area of the shaded region ?
 A(4−3π2)cm2B(2π−4)cm2C(4−2π)cm2Dnone of these
A(4−3π2)cm2B(2π−4)cm2C(4−2π)cm2Dnone of these
In Fig. 15.70, OACB is a quadrant of a circle with centre O and radius 3.5 cm. If OD=2 cm , find the area of the (i) quadrant OACB (ii) shaded region. (FIGURE)
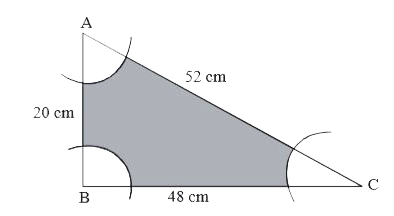
View SolutionWith vertices A, B and C of a triangle ABC as centres, arcs are drawn with radius 6 cm each in fig. If AB= 20 cm, BC= 48 cm and CA= 52 cm, then find the area of the shaded region.
View SolutionIn Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View SolutionIn Fig. 15.63, ABCD is a trapezium with ABDC and ∠BCD=60o . If BFEC is a sector of a circle with centre C and AB=BC=7 cm and DE=4 cm , then find the area of the shaded region (Use π=227 and √3=1.732) .
View SolutionFind the area of the shaded region in Fig. 15.72, if AC=24 cm , BC=10 cm and O is the centre of the circle. (Use π=3.14) (FIGURE)
View SolutionIn Fig. 15.82, ABCD is a rectangle, having AB=20 cm and BC=14 cm . Two sectors of 180o have been cut off. Calculate: (i) the area of the shaded region. (FIGURE) (ii) the length of the boundary of the shaded region.
View Solution
