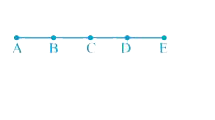
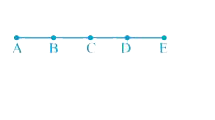
In Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
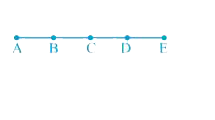
AD = AC + ___________
Step by step video & image solution for In Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then AD = AC + ___________ by Maths experts to help you in doubts & scoring excellent marks in Class 6 exams.
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - GEOMETRYEXERCISE - Exercise (State whether the statements given in questions are true (T) or false (F):)10videos
GEOMETRY
- BOOK - NCERT EXEMPLARCHAPTER - GEOMETRYEXERCISE - Exercise56videos
GEOMETRY
- BOOK - NCERT EXEMPLARCHAPTER - GEOMETRYEXERCISE - Exercise (Out of foure options only one is correct. Write the correct answer.)16videos
GEOMETRY
- BOOK - NCERT EXEMPLARCHAPTER - FRACTIONS AND DECIMALS EXERCISE - ACTIVITY1videos
FRACTIONS AND DECIMALS
- BOOK - NCERT EXEMPLARCHAPTER - INTEGERS EXERCISE - Exercise42videos
INTEGERS
Similar Questions
Knowledge Check
- Question 1 - Select One
If A, B, C and D are four numbers such that A:B=2:3,B:C=4:5,C:D=5:8, then A:D is equal to
A1:3B3:1C2:3D3:2 - Question 2 - Select One
For a triangle ABC,D and E are two points on AB and AC such that AD=14AB,AE=14AC. If BC=12cm, then DE is
Aa) 5 cmBb) 4 cmCc) 3 cmDd) 6 cm - Question 3 - Select One
In ΔABC D and E are the points on sides AB and AC, respectively, such that DE || BC. If AD = 4 cm, BC = 5 cm. DC = 10 cm and AB = 15 cm. then the sum of the lengths of DE and EC is:
AA. 20 cmBB. 15 cmCC. 21 cmDD. 18 cm
In Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
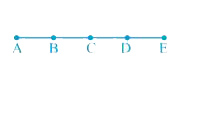
mid point of AE is __________View SolutionIn Fig. 2.15, points A,B,C,D and E are collinear such that AB = BC = CD= DE. Then
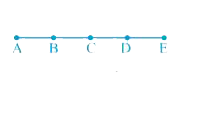
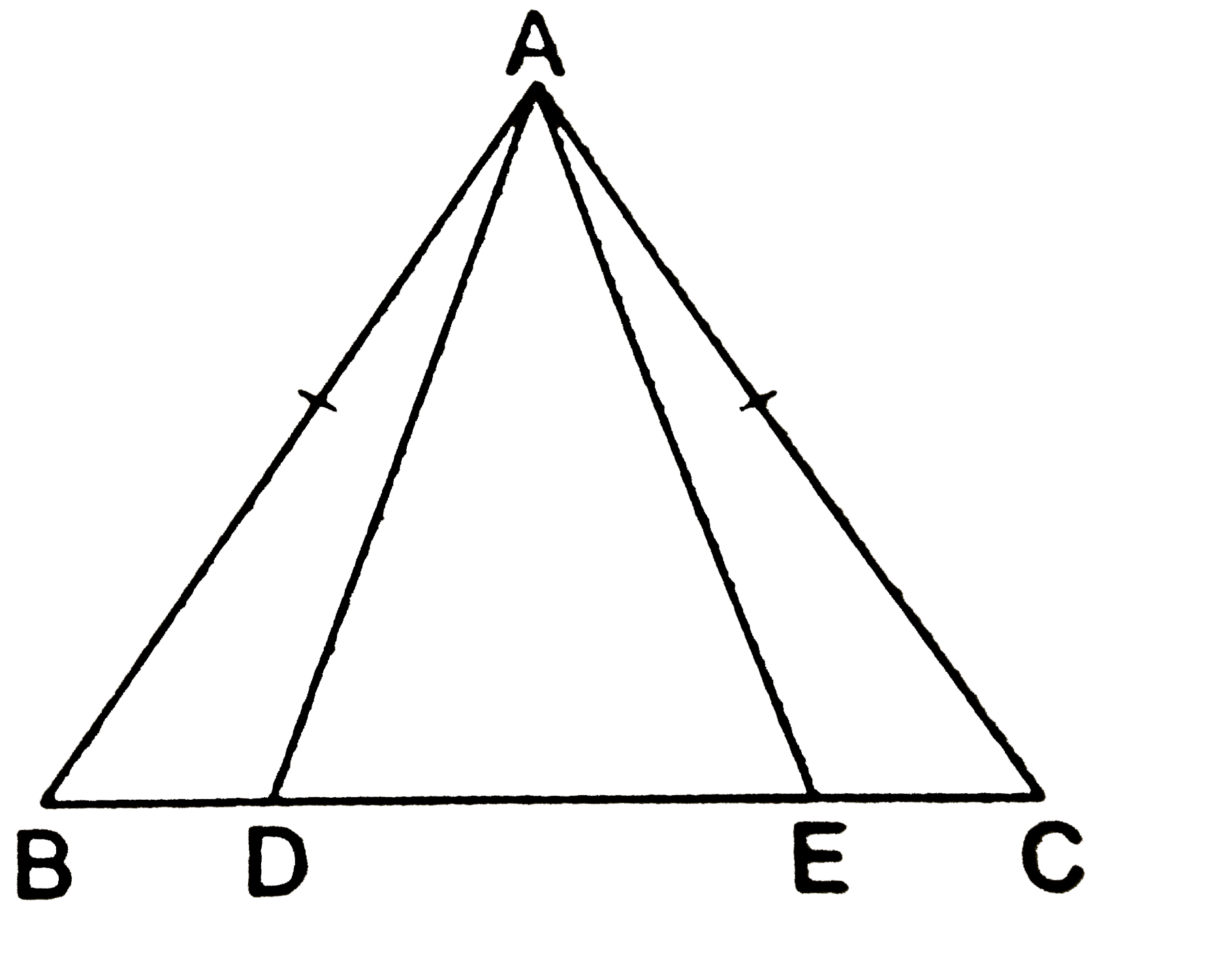
mid point of CE is __________View SolutionIn an isosceles ΔABC with AB = AC, D and E are point on BC such that BE = CD. Show that AD = AE.
 View Solution
View SolutionIn Fig.11, it is given that AB=CD and AD=BC. Prove that ADC≅CBA.
View SolutionIn Figure, AC>AB and D is the point on AC such that AB=AD. Prove that BC>CD
 View Solution
View Solution