In Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that ∠POQ+∠QOR+∠SOR+∠POS=360o
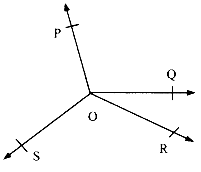
If we extend ray QO to T as shown in figure to point such that QT is a straight line, Then
∠POQ+∠POT=180∘→(1)--> As, angle created by a straight line is always 180∘
∠SOT+∠SOQ=180∘
As, ∠SOQ=∠SOR+∠ROQ
∠SOT+∠SOR+∠ROQ=180∘→(2)
Adding (1) and(2),
∠POQ+∠POT+∠SOT+∠SOR+∠ROQ=360∘
As,∠POT+∠SOT=∠POS,
∠POQ+∠POS+∠SOR+∠ROQ=360∘
Similar Questions
In Figure, OP, OQ, OR and OS are four rays. Prove that ∠POQ+ ∠QOR+ ∠SOR+ ∠POS=3600
View SolutionIn Fig 7.51, PR > PQand PS bisects ∠QPR. Prove that ∠PSR >∠PSQ.
 View Solution
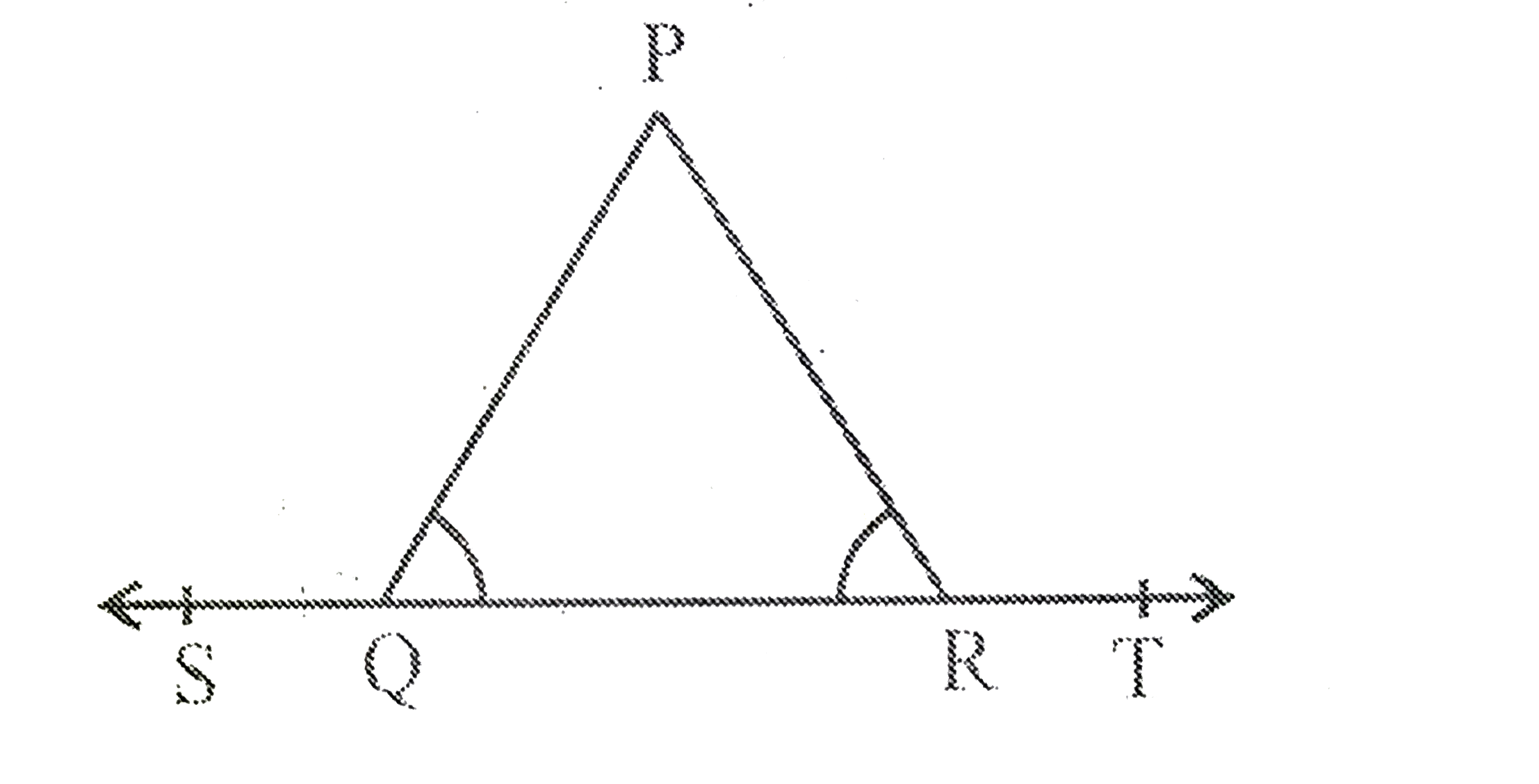
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
 View Solution
View SolutionIn Fig. 10.101, PQ and PR are two tangents to a circle with centre O . If ∠QPR=46o , then ∠QOR equals (a) 67o (b) 134o (c) 44o (d) 46o
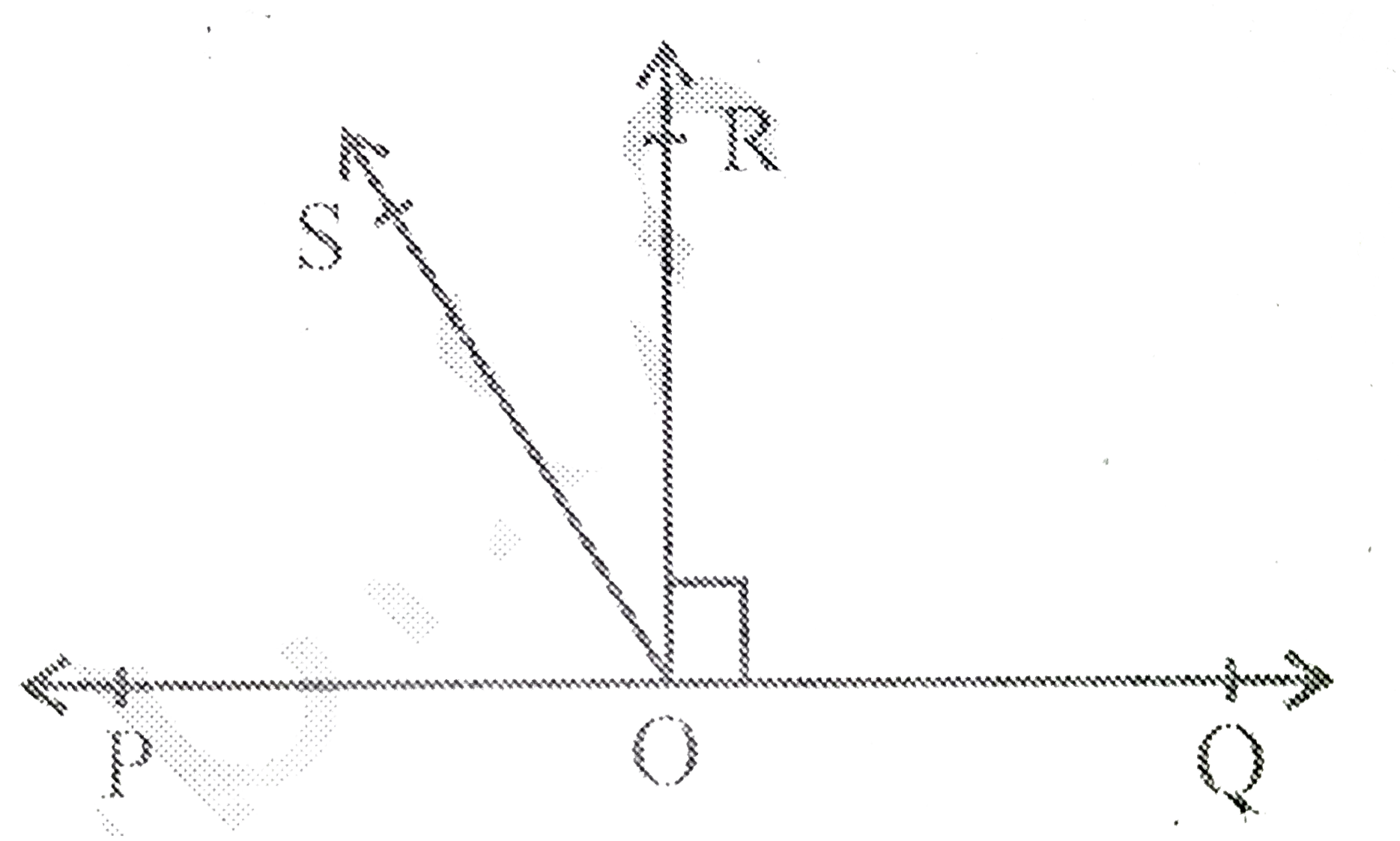
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
 View Solution
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
View SolutionIn Fig. 10.95, PQ and PR are tangents drawn from P to a circle with centre O . If ∠OPQ=35o , then (FIGURE) a=30o, b=60o (b) a=35o, b=55o (c) a=40o, b=50o (d) a=45o, b=45o
View SolutionIn Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ , respectively. If ∠POS=x , find ∠ROT .
View SolutionIn Figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS)
View SolutionIn Figure, ∠PQR= ∠PRQ, then prove that ∠PQS= ∠PRT.
View Solution

