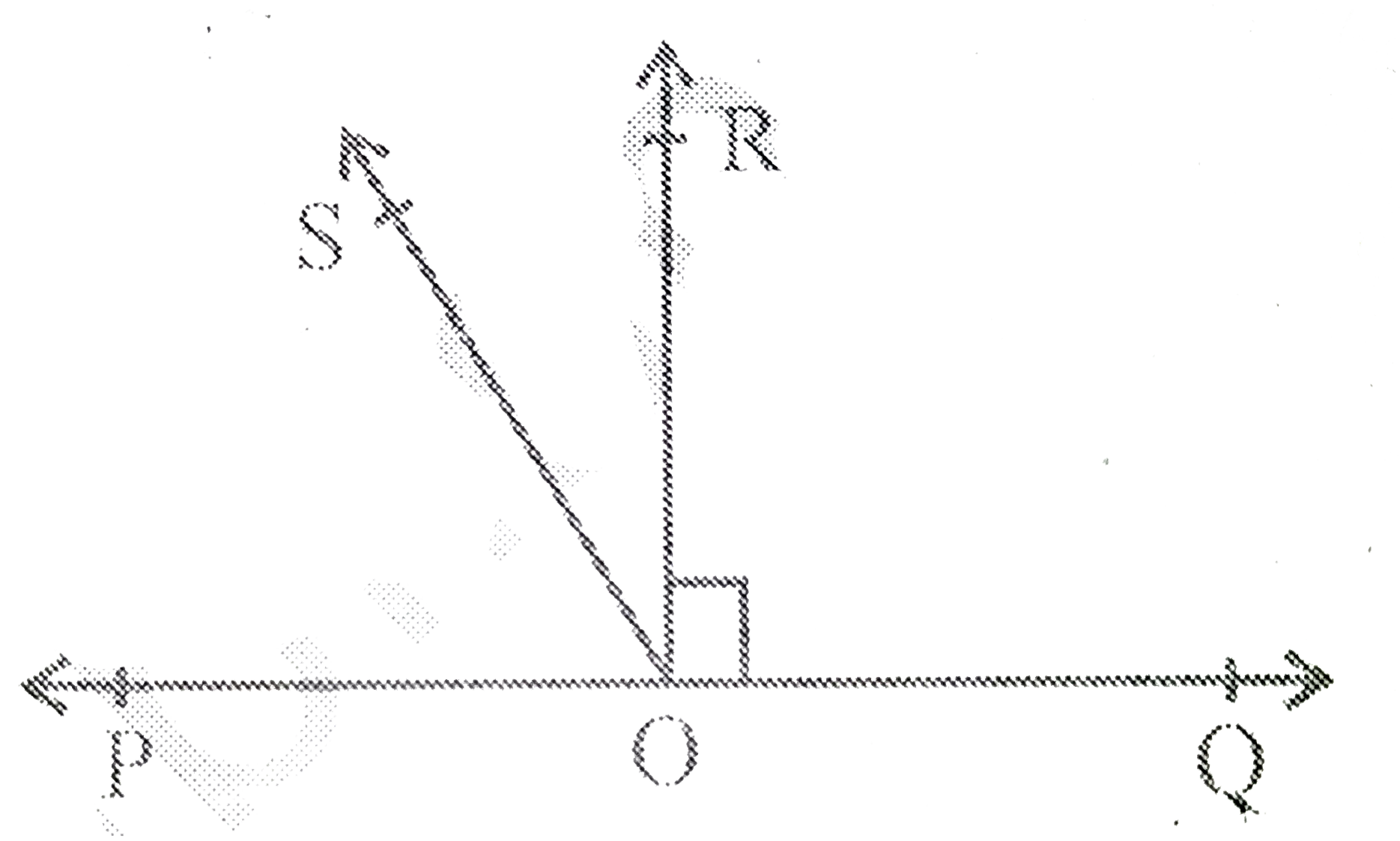
In Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
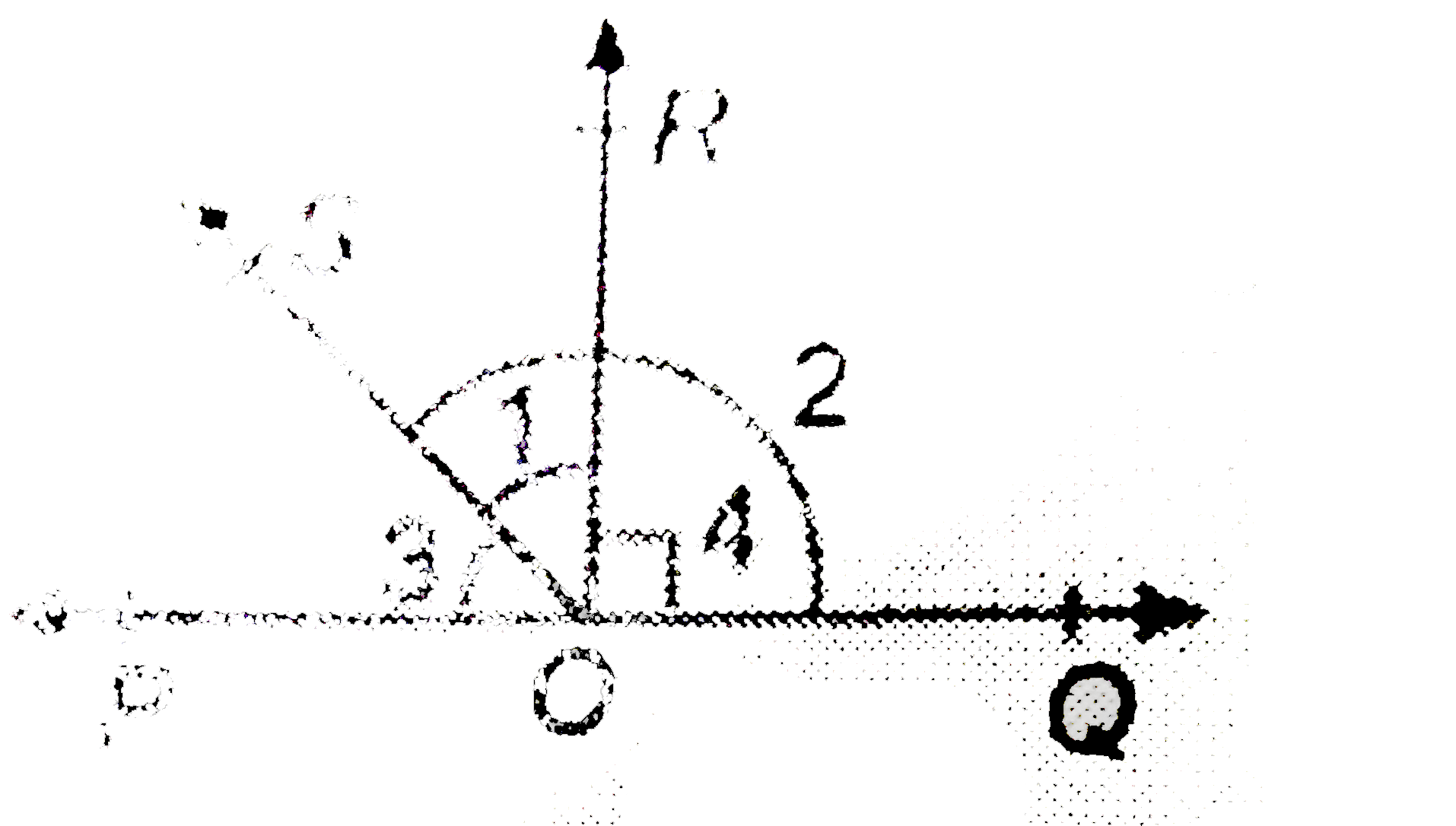
∠POR+∠ROQ=180o
∠ROP=∠ROQ=90o
∠SOQ=anf≤ROS+∠ROQ
∠ROS=∠SOQ−∠ROQ−(1)
∠ROP=∠ROS+∠POS<br>angleROS=angleROP-anglePOS-(2)
adding 1 and 2
∠ROS+∠ROS=∠SOQ+∠ROP−∠ROQ−∠POS
2∠ROS=∠SOQ−∠POS
∠ROS=12(∠SOQ−∠POS)
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - SOLVED EXAMPLES
8 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NCERT ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Exercise 4.1
2 Videos
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.12
1 Videos
Similar Questions
In Figure, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS)
View SolutionIn figure POQ is a line. Raw Oris perpendicular to line PQ .OS is another ray lying between rays OP and OR. Prove that ∠ROS12(∠QOS−∠POS)i.e.,∠1=12(∠2−∠3)
View SolutionIn Figure, POS is a line, find x
View SolutionIn Fig.29, POS is a line, find x.
View SolutionIf PS is the bisector of ∠QPR and PT⊥QR . Show that ∠TPS=12(∠Q−∠R).
View SolutionIn Fig. 6.44, the side QR of PQR is produced to a point S. If the bisectors of ∠PQR\ and∠PRS meet at point T, then prove that ∠QTR=12∠QPR .
View SolutionIn Fig. 6.10, ray OS stands on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ , respectively. If ∠POS=x , find ∠ROT .
View SolutionIn Fig. , the side QR of △ PQR is produced to a point S. If the bisectors of ∠PQR and ∠PRS meet at point T, then prove that ∠QTR=12∠QPR.

View SolutionIn Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that ∠POQ+∠QOR+∠SOR+∠POS=360o
View SolutionIn Fig. 6.11, OP, OQ, OR and OS are four rays. Prove that ∠POQ+∠QOR+∠SOR+∠POS=360o
View Solution
