In Fig. 6.13, lines AB and CD intersect at O. If ∠AOC +∠BOE=70∘and ∠BOD=40∘, find ∠BOE and reflex ∠COE.
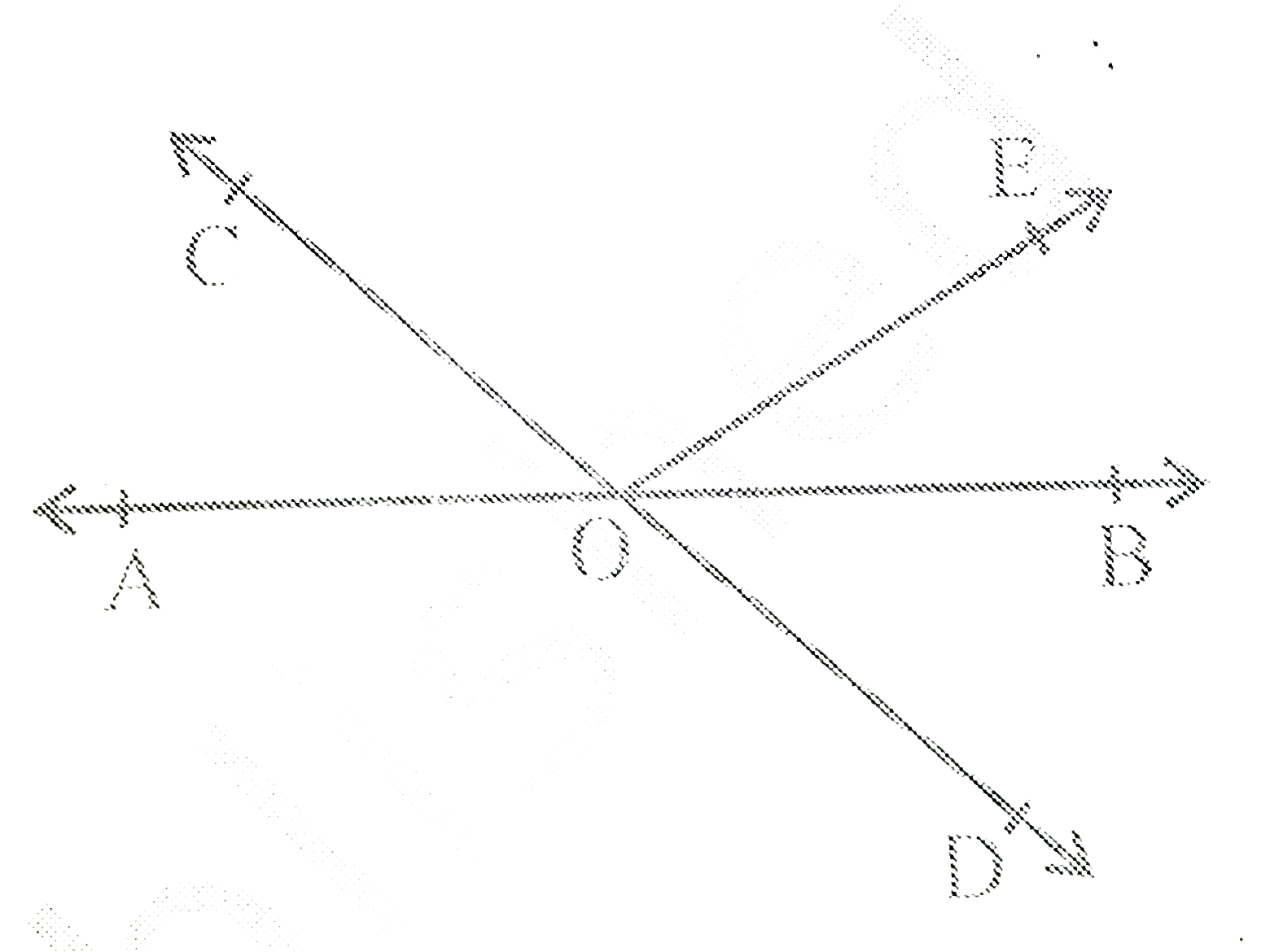
Let ∠AOC=x and ∠BOE=y.
Thenx+y=70∘ ( ∠AOC+∠BOE=70∘)
Let Reflex ∠COE=z
We can see that AB and CD are two intersecting lines, so the pair of angles formed are vertically opposite angles and they are equal.
i.e, ∠AOD=∠BOC and ∠AOC=∠BOD.
Since ∠AOC=xand ∠AOC=∠BOD=40∘
Thus, we can say that x=40∘
Also we know that,
x+y=70∘
40∘+y=70∘
y=70∘−40∘=30∘
∠BOE=30∘
If we consider line AB and ray OD on it, then ∠AOD and ∠BOD are adjacent angles.
∠AOD+∠BOD=180∘
∠AOD+40°=180∘
∠AOD=180∘−40∘
=140∘
Reflex ∠COE=∠AOC+∠AOD+∠BOD+∠BOE
=40∘+140∘+40∘+30∘
=250∘
Thus, ∠BOE=30∘ and the reflex ∠COE=250∘.
Topper's Solved these Questions
Similar Questions
In Figure, lines AB and CD intersect at O.
View SolutionIn fig: 6.14, lines XY and MN intersect at O. If ∠POY=90∘and a:b=2:3, find c.

View SolutionLine segments AB and CD intersect at O such that AC∣∣DB . If ∠CAB=350 and ∠CDB=550 find the ∠BOD.
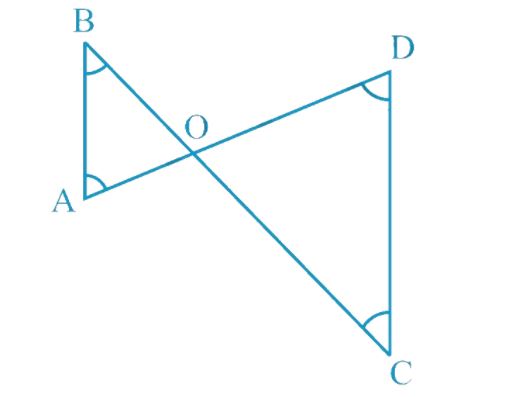
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800
View SolutionThe diagonals of a rectangle ABCD meet at O . If ∠BOC=44∘, find ∠OAD
View SolutionThe diagonals of a parallelogram ABCD intersect at O . If ∠BOC=90∘ and ∠BDC=50∘, then ∠OAB= 40∘ (b) 50∘ (c) 10∘ (d) 900
View SolutionIn figure, ΔODCΔOBA,∠BOC=125oand ∠CDO=70o. Find∠DOC,∠DCOand∠OAB.
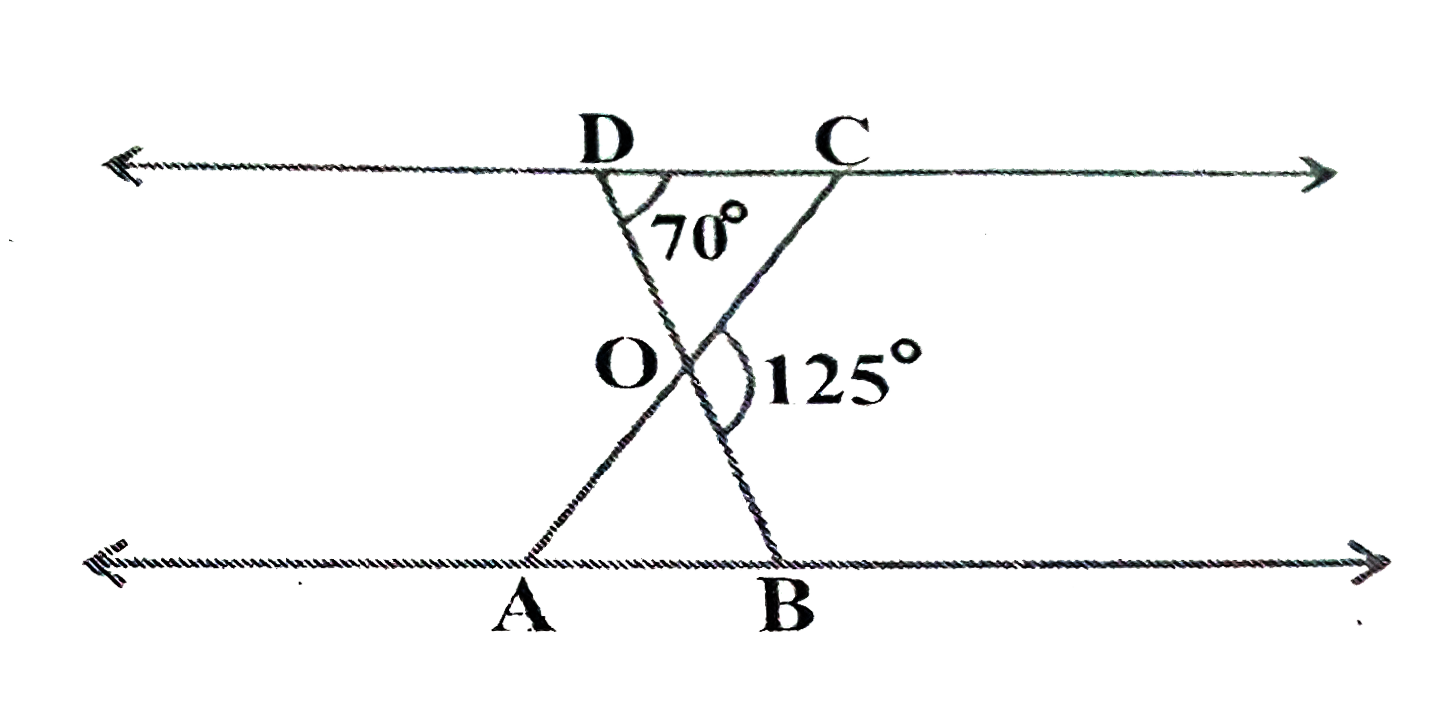
View SolutionABCD is a cyclic quadrilateral whose diagonals intersect at a point E. If ∠DBC = 70o,∠BAC is 30o, find ∠BCD. Further, if AB = BC, find∠ECD.
View SolutionIn Fig.92, AOB is a straight line such that ∠AOC=(3x+10)0, ∠COD=500 and ∠BOD=(x−8)0. The value of x is (a) 32 (b) 36 (c) 42 (d) 52
View SolutionTwo lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
View Solution
