In Figure, ray OS stand on a line POQ. Ray OR and ray OT are angle bisectors of ∠POS and ∠SOQ respectively. If ∠POS=x, find ∠ROT
Video Solution
Text Solution
∠POS+∠SOQ=1800−(1)
∠POSand∠SOQ is linear pair of angles.
∠POR=∠ROS<br>∠SOT+∠TOQ=∠SOQ
∠SOT=∠TOQ
x+∠SOQ=1800
∠SOQ=1800−x−(2)
2∠SOT=1800−x
∠SOT=1800−x2-(3)
∠ROS=∠POS2
∠ROS=x2
∠ROT=∠SOT+∠ROS
180−x2+x2
=900.
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The number of S-O-S and O-H links in H2S2O7 molecule are respectively
A0,2B1,2C2,2D2,1 - Question 2 - Select One
The I.P1's of N,P,O & S are in the order of
AS>P<O>NBN>O>P>SCN>O<P>SDN<O<P<S - Question 3 - Select One
ABCD is a parallelogram and O is the point of intersection of its diagonals. If points P, Q, R, S are the mid-points of OA, PB, QC, RD respectively, then the points Q, O, S
Aforms a triangleBare non-coplanarCare collinearDare non-collinear
In Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
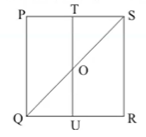 View Solution
View SolutionIn Fig. 6.17, POQ is a line. Ray OR is perpendicular to line PQ. OS is another ray lying between rays OP and OR. Prove that ∠ROS=12(∠QOS−∠POS).
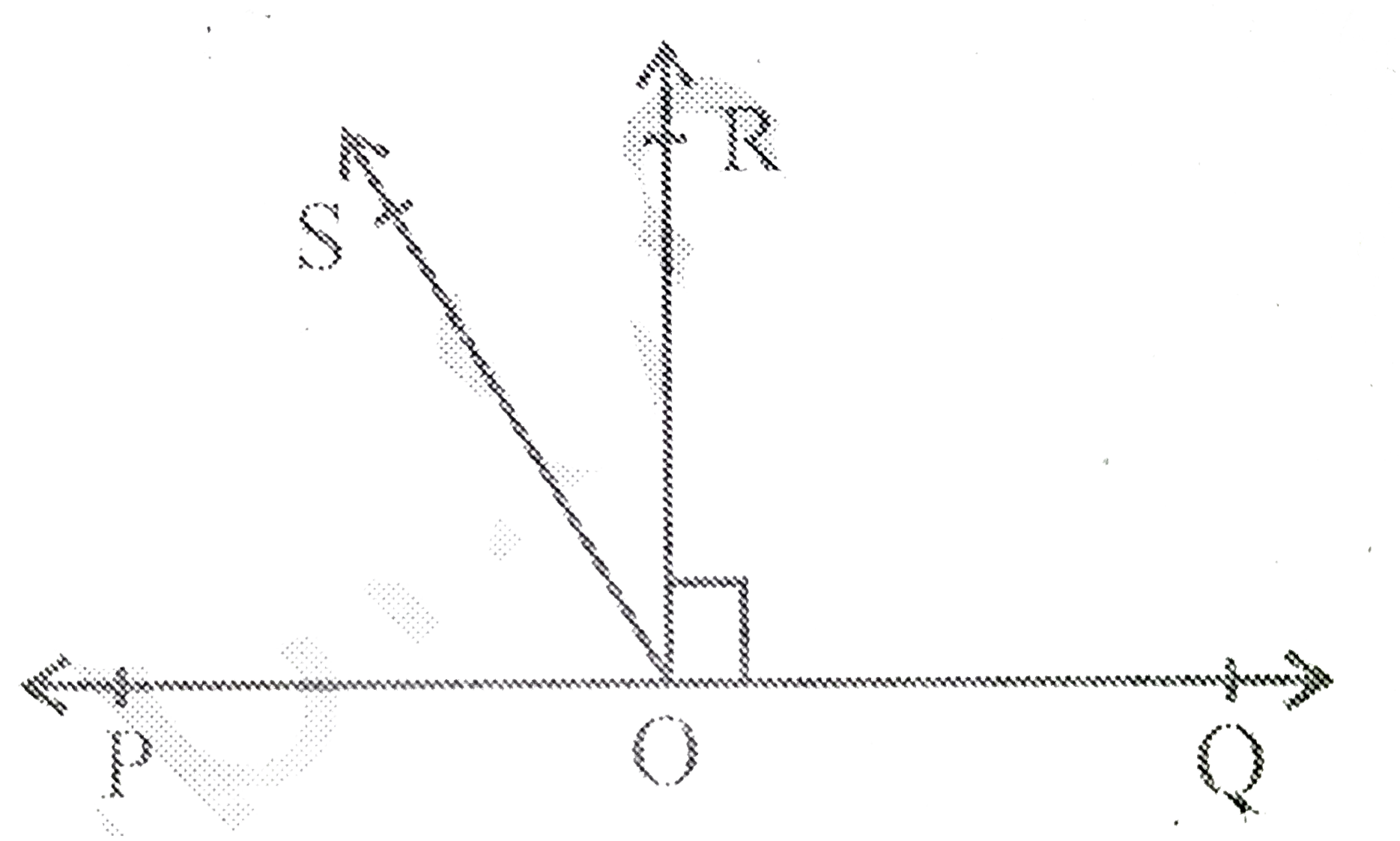 View Solution
View SolutionABCD is a parallelogram whose AC and BD intersect at O. A line through O intersects AB at P and DC at Q. Prove that ar ( POA)= ar ( QOC).
View SolutionIn Fig. 10.37, ∠PQR = 100∘, where P, Q and R are points on a circle with centre O. Find ∠OPR.
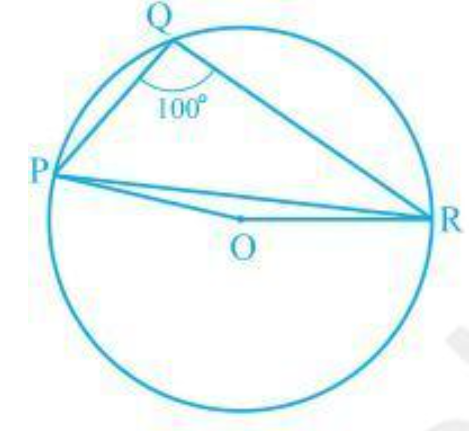 View Solution
View SolutionLet O be the origin, and OX,OY,OZ be three unit vectors in the direction of the sides QR , RP , PQ , respectively of a triangle PQR. |OX×OY|= s∈(P+R) (b) sin2R (c)sin(Q+R) (d) sin(P+Q).
View Solution

