In Fig. AC and AD are tangent to a circle at C and D respectively. If ∠BCD=44∘, then find ∠CAD,∠ADC,∠CBD and ∠ACD.
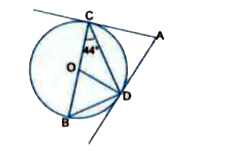
Step by step video, text & image solution for In Fig. AC and AD are tangent to a circle at C and D respectively. If angleBCD = 44^(@), then find angleCAD, angleADC, angleCBD and angleACD. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MODEL QUESTION PAPER -7 BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER -7 EXERCISE - SECTION -D
8 Videos
- MODEL QUESTION PAPER -7 BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER -7 EXERCISE - SECTION -B
6 Videos
- MODEL QUESTION PAPER -2 [UNSOLVED]BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER -2 [UNSOLVED]EXERCISE - SECTION-D
10 Videos
- MODEL QUESTION PAPER 3[UNSOLVED]BOOK - VK GLOBAL PUBLICATIONCHAPTER - MODEL QUESTION PAPER 3[UNSOLVED]EXERCISE - SECTION D
8 Videos
Similar Questions
Knowledge Check
BC, AB and AC are tangents to the circle at D, E and F respectively. ∠EBD=x∘,∠FCD=y∘. Then ∠ EDF equals
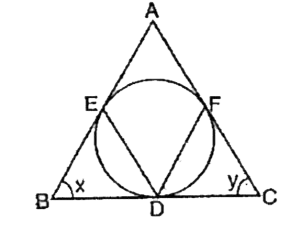 Ax + yBx2−yC90∘−(x+y)Dx+y2
Ax + yBx2−yC90∘−(x+y)Dx+y2In the figure , if AD, AE and BC are tangent to the circle at D,E and F , respectively , then
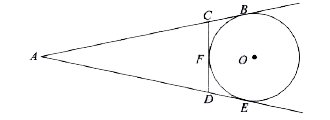 AAD=AB+BC+CAB2AD=AB+BC+CACAD2=AB+BC+CADAD4=AB+BC+CA
AAD=AB+BC+CAB2AD=AB+BC+CACAD2=AB+BC+CADAD4=AB+BC+CAIn the given figure, AB and AC are tangents to the circle at B and C respectively and O is the centre of the circle, then x equals
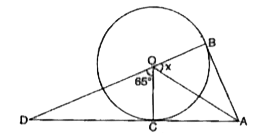 A65∘B32.5∘C57.5∘D45∘
A65∘B32.5∘C57.5∘D45∘
Two same circles of radius 5 cm has a direct tangent AB and a transversal CD which touch circle at A, B and C, D respectively. If CD = 24 cm then find the length of AB (in cm)?
View Solution
In the figure above ,AD=AC=BD. The point B, D and C are collinear. If ∠CAD=80∘, then find ∠DAB.
View Solution
In the above figure, O is the centre of the circle AB,AD and CD are the chords . If ∠ADC=130∘ then fid ∠ACB.
View SolutionIf Fig , AOB is diameter of a circle with centre O and AC is a tangent to the circle at A . If ∠BOC=130∘ , then find ∠ACO .

View SolutionIf ΔABC,∠A=52∘, Its sides AB and AC are produced to the points D and E respectively. If the bisectors of the ∠CBDand∠BCE meet at point O, then ∠BOC is equal to:
View Solution

