In Fig.6.45,O is a point in the interior of a triangle ABC,OD⊥BC,OE⊥ACandOF⊥AB.Show that
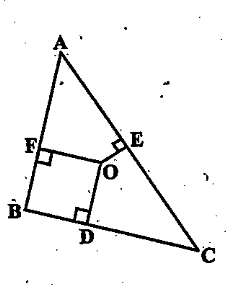 (i)OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2Solution in Assamese
(i)OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2Solution in Assamese
Step by step video & image solution for In Fig.6.45,O is a point in the interior of a triangle ABC,OD_|_BC,OE_|_AC and OF_|_AB.Show that (i)OA^2+OB^2+OC^2-OD^2-OE^2-OF^2=AF^2+BD^2+CE^2 by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The length of a diagonal of a square is 16cm. Find the length of the side of it.
View Solutiona number is selected from 1,2,3,....,15. what is the probability that the number is a multiple of 4
View SolutionWhich of the following is quadratic equation:
x2+√2x+3=0.
View SolutionFrom a point O in the interior of a ABC , perpendiculars OD, OE and OF are drawn to the sides BC, CA and AB respectively. Prove that: (i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2 (ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionMatch the following Column A to Column B

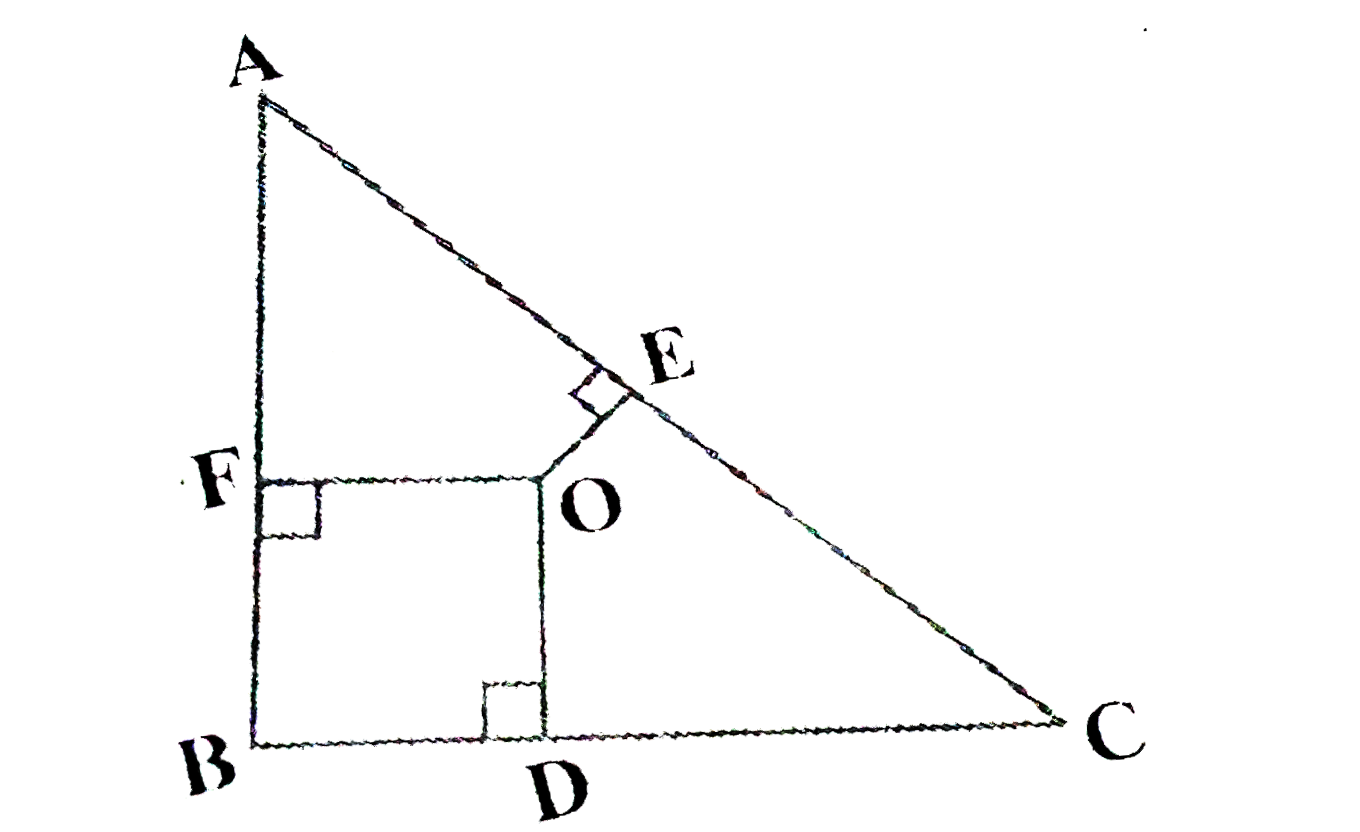
View Solutionआकृति 6 . 54 में ΔABC के अभ्यन्तर में स्थित कोई बिंदु O है तथा OD⊥BC,OE⊥AC और OF⊥AB है दर्शाइए कि
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionO is a point in the interior of ΔABC,OD⊥BC,OE⊥ACandOF⊥AB, as shown in the figure,
Prove that :
(i)OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AD2+BF2+CD2
View Solution△ABC के एक अन्तः बिंदु O से, भुजा BC,CA तथा AB पर लम्ब क्रमशः OD,OE व OF खींचे गये है | सिद्ध कीजिए कि
(i) AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
View SolutionΔABC के अंदर बिंदु O से भुजाओ BC,CA और AB पर क्रमश: लंब OD,OE और OF डाले गए है। सिद्ध कीजिए कि
AF2+BD2+CE2=OA2+OB2+OC2−OD2−OE2−OF2.
View SolutionIn Fig. 2.54, o is a point in the interior of a triangle ABC,OD⊥BC,OE⊥ACandof⊥AB. Show that
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2,
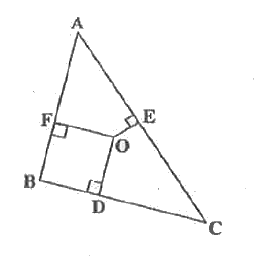
View SolutionIn fig . O is a point in the interior of a triangle ABC , OD ⊥BC,OE⊥ACandOF⊥AB . Show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2+AE2+CD2+BF2 .
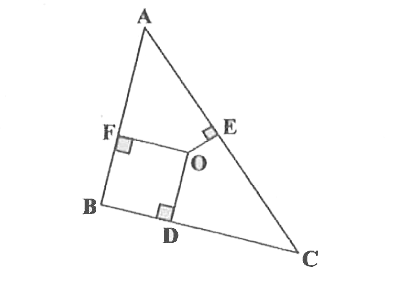
View Solutionత్రిభుజము ABC అంతరంలో ఏదైనా బిందువు 'O' OD⊥BC,OE⊥AC మరియు OF⊥AB అయిన OA2+OB2+OC2−OD2−OE2−OE2=AE2+BD2+CE2
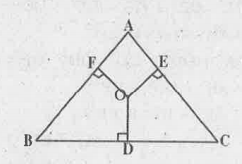
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
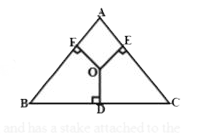
View Solution‘O’ is any point in the interior of a triangle ABC. If OD⊥BC,OE⊥AC and OF ⊥ AB, show that
(i) OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BE2.
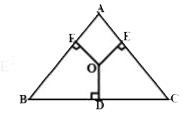
View SolutionIn the figure given below, O is point in the interior of a triangle ABC, OD⊥BC, OE⊥AC and OF⊥AB. Show that
(i) OA2+OB2+OC2+OD2−OE2−OF2=AR2+BD2+CE2
(ii) AF2+BD2+CE2=AE2+CD2+BF2
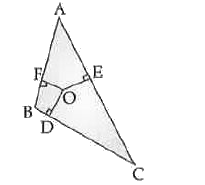
View SolutionIn the given figure, O is a point in the interior of a DeltaABC, OD⊥BC,OE⊥AC and OF⊥AB. Show that :
OA2+OB2+OC2−OD2−OE2−OF2=AF2+BD2+CE2.
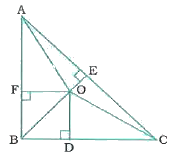
View Solution
