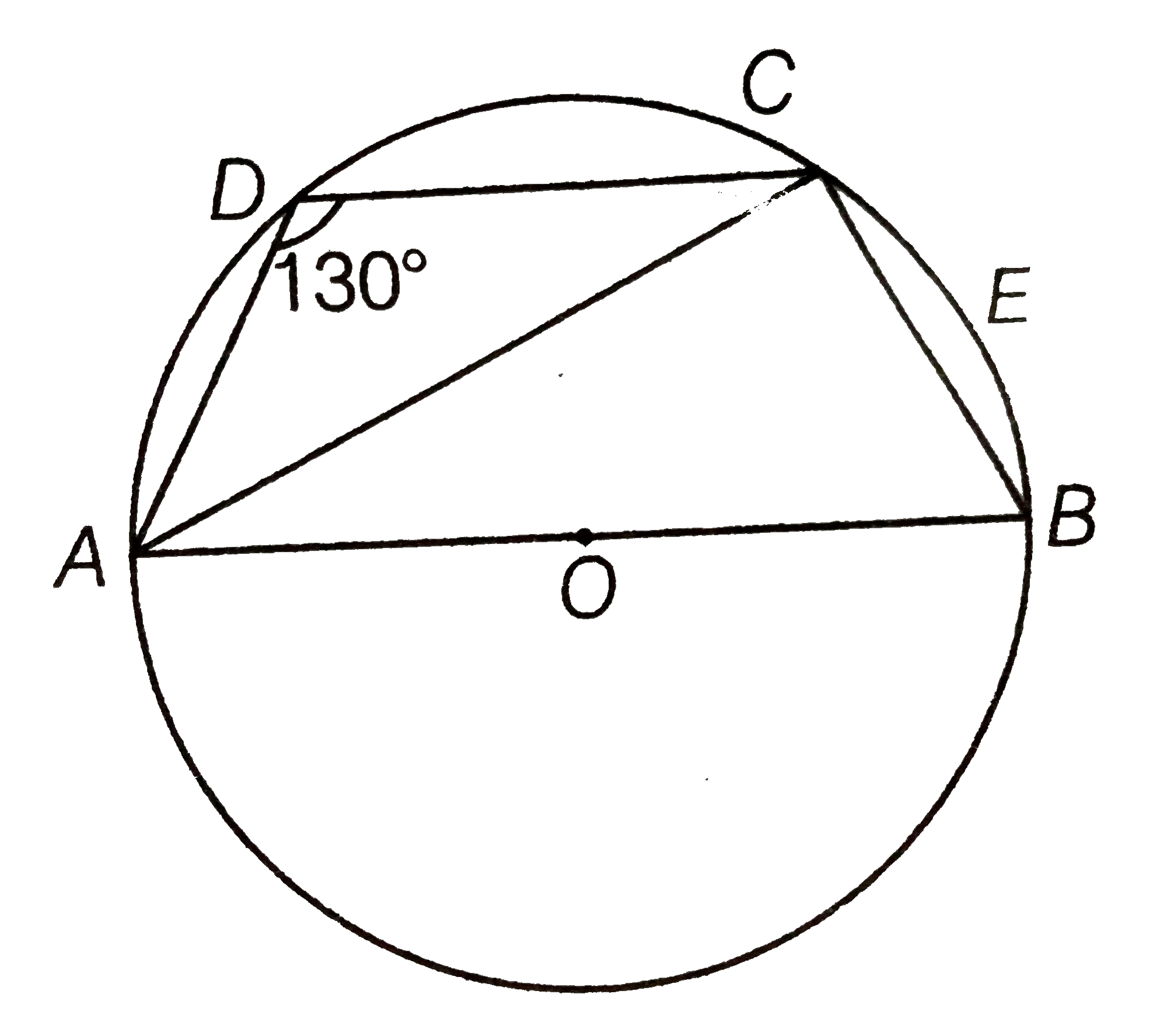
In Figure, ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If (∠ADC)=1300,find ∠BAC
Video Solution
Text Solution
Draw a quadrilateral ABCD inscribed in a circle having centre O. Given, ∠ADC=130∘
Since, ABCD is a quadrilateral inscribed in a circle, therefore ABCD becomes a cyclic quadrilateral.
∵ Since, the sum of opposite angles of a cyclic quadrilateral is 180∘.
∴∠ADC+∠ABC=180∘
⇒130∘+∠ABC=180∘
⇒∠ABC=50∘
Since, AB is a diameter of a circle, then AB subtends an angle to the circle is right angle.
∴∠ACB=90∘
In ΔABC,∠BAC+∠ACB+∠ABC=180∘ [by angle sum property of a triangle]
⇒∠BAC+90∘+50∘=180∘
⇒∠BAC=180∘−(90∘+50∘)
=180∘−140∘=40∘

|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
ABCD is a cyclic quadrilateral whose side AB is a diameter of the circle through A, B, C, D. If ∠ADC=130∘, find ∠BAC.
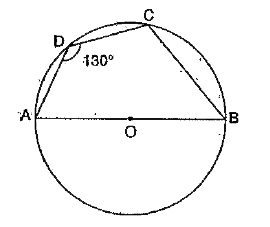 A40∘B50∘C60∘D30∘
A40∘B50∘C60∘D30∘If ABCD is a cyclic quadrilateral with ∠A=50∘,∠B=80∘, then Cand∠D are
A100∘,130∘B115∘,115∘C110∘,120∘D130∘,100∘In a cyclic quadrilateral ABCD∠A+∠B+∠C+∠D=?
AA)90∘BB)360∘CC)180∘DD)120∘
In Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View SolutionABCD is a cyclic quadrilateral whose diagonals ACandBD intersect at P . If AB=DC, Prove that : PAB≅PDC PA=PDandPC=PB ADBC
View SolutionIna cyclic quadrilateral
∠A+∠C=∠B+∠D=?
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIn a cyclic quadrilateral ABCD, if AB ∣∣ CD and ∠B=70∘, find the remaining angles.
View Solution
