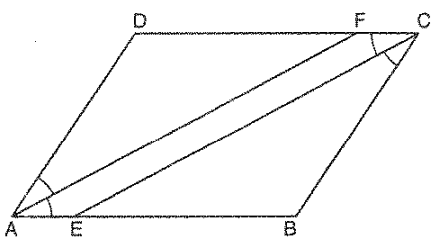
In Figure, ABCD
is a parallelogram, CE
besects ∠C and AF
bisects ∠A.
In each of the following, if the statement is
true, give a reason for the same:
∠A=∠C
(ii) ∠FAB=12∠A
∠DCE=12∠C
(iv) ∠CEB=∠FAB
ceAF
Step by step video & image solution for In Figure, A B C D is a parallelogram, C E besects /_C\ a n d\ A F bisects /_Adot In each of the following, if the statement is true, give a reason for the same: /_A=/_C (ii) /_F A B=1/2/_A /_D C E=1/2/_C (iv) /_C E B=/_F A B c e A F by Maths experts to help you in doubts & scoring excellent marks in Class 8 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a parallelogram, CE besects ∠C and AF bisects ∠A. In each of the following, if the statement is true, give a reason for the same: ∠A=∠C (ii) ∠FAB=12∠A ∠DCE=12∠C (iv) ∠CEB=∠FAB ceAF

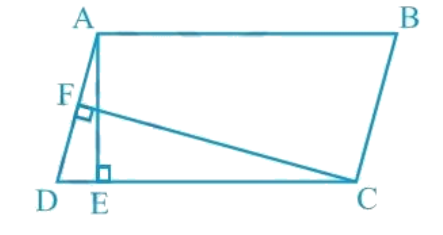
View SolutionIn Figure, ABCD is a parallelogram, AE ⊥DC and CF⊥AD . If AB=16CM, AE=8cm and CF=10cm, find AD
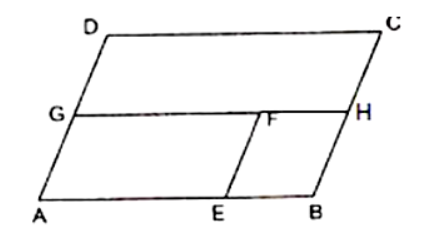
View SolutionIn Figure, ABCD and AEFG are two parallelograms. If ∠C=580, find ∠F
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
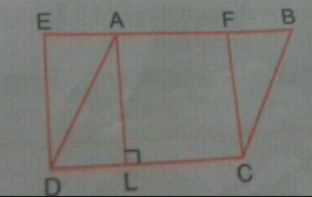
View SolutionIn the following figure, ABCD is a parallelogram and EFCD is a rectangle. Also, AL⊥DC. Prove that
(i) ar(ABCD)=ar(EFCD)
(ii) ar(ABCD)=DC×AL.
View SolutionABCD is a parallelogram. AD is a produced to E so that DE=DC and EC produced meets AB produced in F. Prove that BF=BC.
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
View SolutionABCD is a parallelogram and EandF are the centroids of triangles ABD and BCD respectively, then EF= (a)AE (b) BE (c) CE (d)DE
View Solution
