In Figure, ABCD is a parallelogram in which ∠DAB=750, ∠DBC=600. Calculate ∠CDB and ∠ADB.
To solve the problem step by step, we will use the properties of a parallelogram and the relationships between the angles.
1. Identify the Given Angles:
- We have a parallelogram ABCD.
- Given:
- Angle DAB = 75°
- Angle DBC = 60°
2. Use the Property of Opposite Angles in a Parallelogram:
- In a parallelogram, opposite angles are equal.
- Therefore, angle C (which is opposite to angle A) will also be:
Angle C=Angle DAB=75°
3. Calculate the Remaining Angles in Triangle BCD:
- In triangle BCD, the sum of the angles is 180°.
- We know:
- Angle DBC = 60°
- Angle C = 75°
- Let angle CDB be denoted as x.
- Therefore, we can write the equation:
Angle DBC+Angle C+Angle CDB=180°
- Substituting the known values:
60°+75°+x=180°
4. Solve for Angle CDB:
- Combine the known angles:
135°+x=180°
- Now, isolate x:
x=180°−135°=45°
- Thus, angle CDB = 45°.
5. Calculate Angle ADB:
- Angle ADB is equal to angle DBC because they are alternate angles.
- Therefore:
Angle ADB=Angle DBC=60°
Final Answers:
- Angle CDB = 45°
- Angle ADB = 60°
- We have a parallelogram ABCD.
- Given:
- Angle DAB = 75°
- Angle DBC = 60°
- In a parallelogram, opposite angles are equal.
- Therefore, angle C (which is opposite to angle A) will also be:
Angle C=Angle DAB=75°
- In triangle BCD, the sum of the angles is 180°.
- We know:
- Angle DBC = 60°
- Angle C = 75°
- Let angle CDB be denoted as x.
- Therefore, we can write the equation:
Angle DBC+Angle C+Angle CDB=180°
- Substituting the known values:
60°+75°+x=180°
- Combine the known angles:
135°+x=180°
- Now, isolate x:
x=180°−135°=45°
- Thus, angle CDB = 45°.
- Angle ADB is equal to angle DBC because they are alternate angles.
- Therefore:
Angle ADB=Angle DBC=60°
- Angle CDB = 45°
- Angle ADB = 60°
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD

View SolutionABCD is a parallelogram in which ∠A=70∘ Compute ∠B, ∠C and ∠D
View SolutionABCD is a parallelogram in which ∠A=70∘. Compute ∠B, ∠C and ∠D.
View SolutionIn Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD
View SolutionIn a parallelogram ABCD , if ∠DAB=75∘and ∠DBC=60∘, then ∠BDC=(a) 75∘ (b) 60∘ (c) 45∘ (d) 55∘
View SolutionIn Figure, ABC is a triangle in which ∠B=2∠C . D is a point on side BC such that AD bisects ∠BAC and AB=CD.BE is the bisector of ∠B . The measure of ∠BAC is
(a) 720
(b) 730
(c) 740
(d) 960

View SolutionIn Figure, ABCD and AEFG are two parallelograms. If ∠C=580, find ∠F
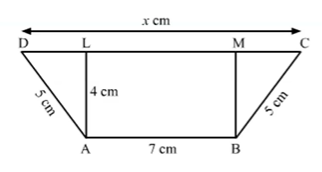
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
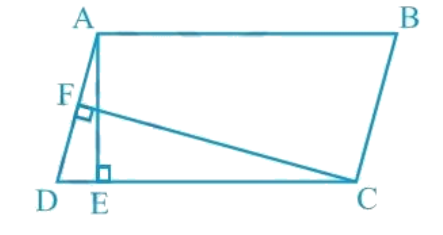
View SolutionIn Figure, ABCD is a parallelogram, AE ⊥DC and CF⊥AD . If AB=16CM, AE=8cm and CF=10cm, find AD
View SolutionIn Figure, ABCD is a trapezium in which ABCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D ABC≅BAD diagonal AC=diagonalBD
View Solution
