In Figure, ABCD is a trapezium in which ABCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D ABC≅BAD diagonal AC=diagonalBD
Given ABCD is trapezium where AD=BC.
(i) To prove: ∠A=∠B
we can see that AECD is a parallelogram, so sum of adjacent angles =180∘
∠A+∠E=180∘
∠A+x=180∘
∠A=180∘−x=∠B
Hence proved.
(ii) To prove: ∠C=∠D
sum of adjacent angles in parallelogram is π, so
∠D∠C+180∘−2x=180∘
∠C+∠D=2x
Now
∠B+∠C=180∘
180∘−x+∠C=180∘=0 ∠C=x, so
∠D=xAnd ∠C=∠D
Hence proved.
(iii) △ABC=△BAD
side AB is common.
AD=BC (given)
so the angle including both the sides is also same,
∠A=∠B. So
△ABC=△BAD (By SAS congruent Rule)
Hence proved.
(iv) As △ABC=△BAD
The third side of both triangles i.e. diagonals are equal AC=BD
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(AOD)=ar(BOC).
 View Solution
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD
 View Solution
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣DC, DC is produced to E such that CE=AB, prove that ar(ABD)=ar (BCE). Construction: Draw DM on BA produced and BN⊥DC
 View Solution
View SolutionIn figure, ABC is triangle in which ∠ABC=90∘and AD⊥CBproduced. Prove that AC2=AB2+BC2−2BC.BD.
 View Solution
View SolutionIn Figure, ABCD is a trapezium in which AB=7cm, AD=BC=5cm, DC=x cm, and distance between AB and DC is 4cm . Find the value of x and area of trapezium ABCD
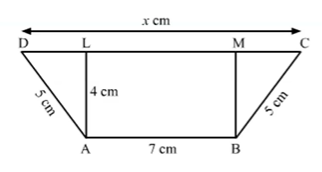 View Solution
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
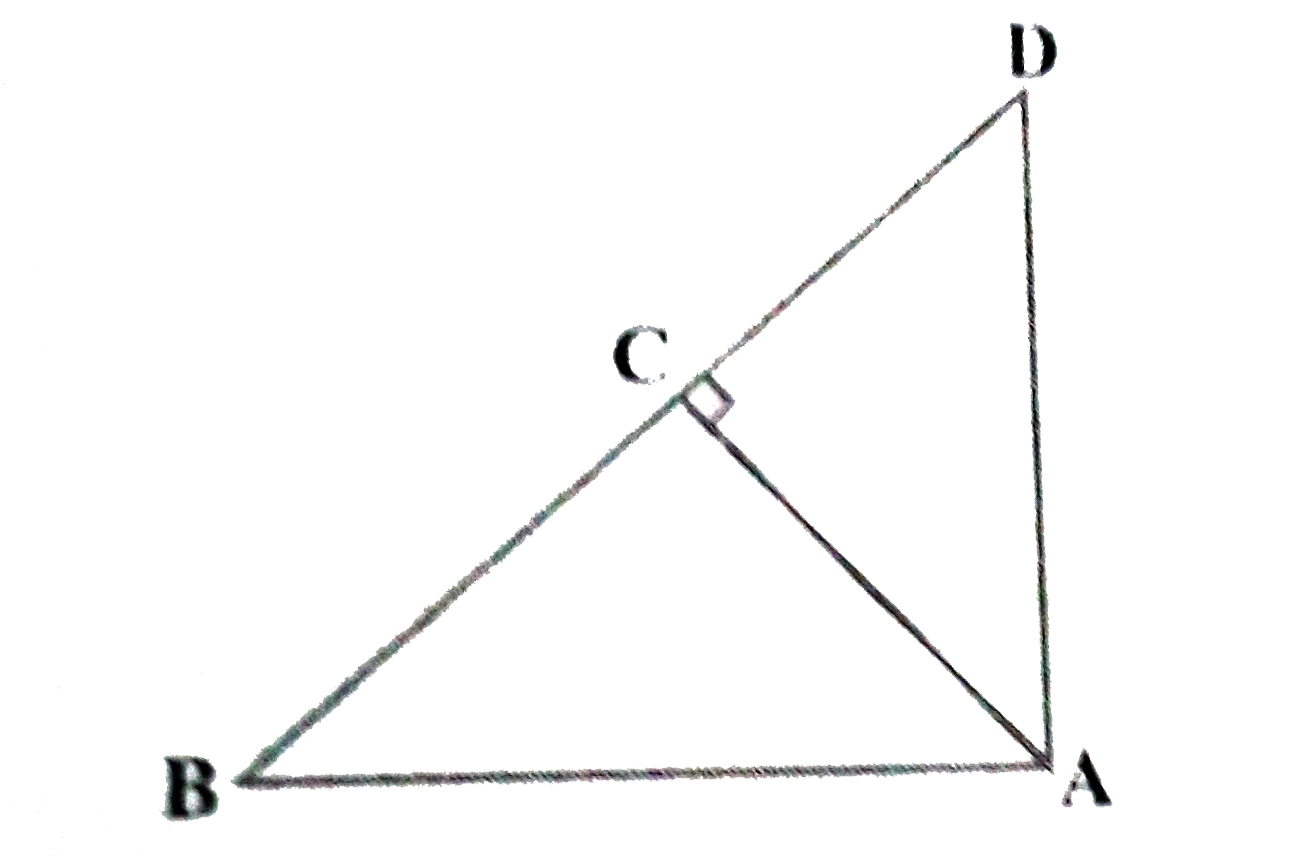 View Solution
View SolutionIn Figure, it is given that AB=BC and AD=EC. Prove that abe ≅CBD (ii) BD=BE
 View Solution
View SolutionIn Figure, ABCD is a rectangle in which diagonal AC is produced to E. If ∠ECD=1460, find ∠AOB
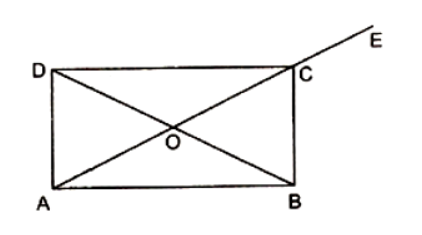 View Solution
View SolutionABCD is a trapezium in which ABCD . The diagonals AC and BD intersect at O . Prove that (i) AOBCOD (ii) If OA=6cm , OC=8cm , Find: Area (AOB)Area (COD) (b) Area (AOD)Area (COD)
View Solution

