In Figure, ABCD
is a trapezium in which AB∣∣CD
and AD=BC.
Show that :
(i) ∠A=∠B
(ii) ∠C=∠D
(iii) ABC≅BAD
(iv) diagonal AC=diagonalBD
To solve the problem step by step, we will demonstrate each part of the question systematically.
Given:
- Trapezium ABCD where AB || CD
- AD = BC
To Show:
1. ∠A = ∠B
2. ∠C = ∠D
3. Triangle ABC ≅ Triangle BAD
4. Diagonal AC = Diagonal BD
Step 1: Show that ∠A = ∠B
1. Construction: Extend line BA to point E such that CE is parallel to AD.
2. Reasoning: Since AB || CD and CE is parallel to AD, by the Alternate Interior Angles Theorem, we have:
- ∠A + ∠2 = 180° (Interior angles on the same side of transversal AD)
- ∠B + ∠1 = 180° (Linear pair)
3. Since AD = BC (given), we can say that ∠1 = ∠2 (angles opposite to equal sides).
4. Substituting: From the above equations, we have:
- ∠A = 180° - ∠2
- ∠B = 180° - ∠1
5. Conclusion: Since ∠1 = ∠2, it follows that ∠A = ∠B.
Step 2: Show that ∠C = ∠D
1. Using the properties of parallel lines: Since AB || CD and AD is a transversal:
- ∠A + ∠B = 180° (Adjacent angles)
- ∠C + ∠D = 180° (Adjacent angles)
2. From Step 1, we have ∠A = ∠B.
3. Substituting: Therefore, ∠D = 180° - ∠A = 180° - ∠B = ∠C.
4. Conclusion: Thus, ∠C = ∠D.
Step 3: Show that Triangle ABC ≅ Triangle BAD
1. Using the congruence criteria:
- AD = BC (given)
- AB = AB (common side)
- ∠ABC = ∠BAD (from Step 1)
2. By SAS (Side-Angle-Side) Congruence Criterion:
- We have two sides and the included angle equal for both triangles.
3. Conclusion: Therefore, Triangle ABC ≅ Triangle BAD.
Step 4: Show that Diagonal AC = Diagonal BD
1. By CPCT (Corresponding Parts of Congruent Triangles): Since Triangle ABC ≅ Triangle BAD, we can conclude:
- AC = BD.
2. Conclusion: Therefore, diagonal AC = diagonal BD.
Final Conclusion:
We have shown that:
1. ∠A = ∠B
2. ∠C = ∠D
3. Triangle ABC ≅ Triangle BAD
4. Diagonal AC = Diagonal BD
- Trapezium ABCD where AB || CD
- AD = BC
1. ∠A = ∠B
2. ∠C = ∠D
3. Triangle ABC ≅ Triangle BAD
4. Diagonal AC = Diagonal BD
2. Reasoning: Since AB || CD and CE is parallel to AD, by the Alternate Interior Angles Theorem, we have:
- ∠A + ∠2 = 180° (Interior angles on the same side of transversal AD)
- ∠B + ∠1 = 180° (Linear pair)
3. Since AD = BC (given), we can say that ∠1 = ∠2 (angles opposite to equal sides).
4. Substituting: From the above equations, we have:
- ∠A = 180° - ∠2
- ∠B = 180° - ∠1
5. Conclusion: Since ∠1 = ∠2, it follows that ∠A = ∠B.
- ∠A + ∠B = 180° (Adjacent angles)
- ∠C + ∠D = 180° (Adjacent angles)
2. From Step 1, we have ∠A = ∠B.
3. Substituting: Therefore, ∠D = 180° - ∠A = 180° - ∠B = ∠C.
4. Conclusion: Thus, ∠C = ∠D.
- AD = BC (given)
- AB = AB (common side)
- ∠ABC = ∠BAD (from Step 1)
2. By SAS (Side-Angle-Side) Congruence Criterion:
- We have two sides and the included angle equal for both triangles.
3. Conclusion: Therefore, Triangle ABC ≅ Triangle BAD.
- AC = BD.
2. Conclusion: Therefore, diagonal AC = diagonal BD.
We have shown that:
1. ∠A = ∠B
2. ∠C = ∠D
3. Triangle ABC ≅ Triangle BAD
4. Diagonal AC = Diagonal BD
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a trapezium in which ABllCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D (iii) A B C~= B A D(iv)DiagonalA C=diagnol B D
View SolutionIn Figure, ABCD is a trapezium in which ABCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D ABC≅BAD diagonal AC=diagonalBD
View SolutionIf ABCD is a quadrilateral in which ABCD and AD=BC, prove that ∠A =∠B .
View SolutionIn figure, ABCD is a trapezium in which AB∣∣CD . Prove that: ar(△AOD)=ar(△BOC).
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: (i) ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD
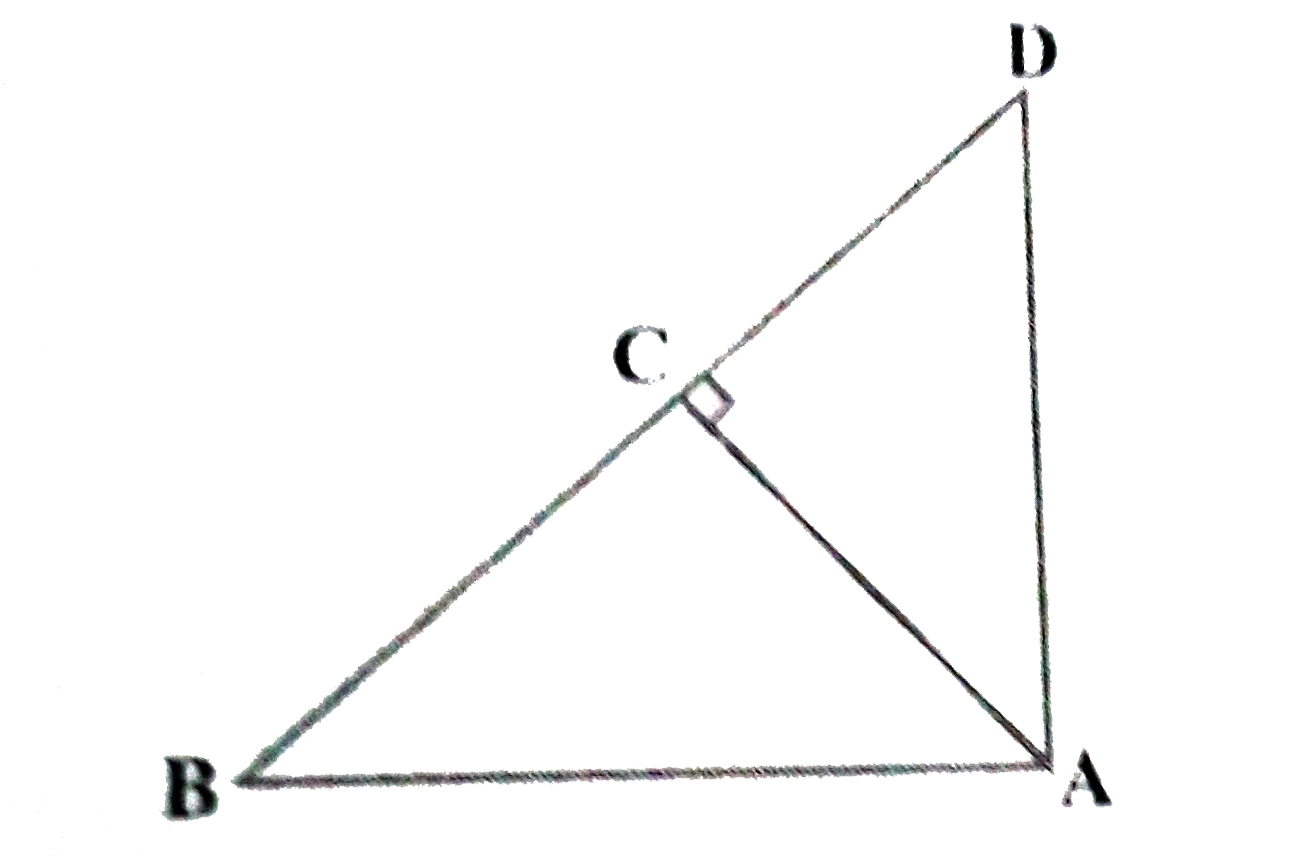
View SolutionIn Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
 View Solution
View SolutionIn Figure, ABCD is a trapezium with AB∣∣DC . If △AED is similar to △BEC , prove that AD=BC .
View SolutionIn Figure, AD and BE are respectively perpendiculars to BC and AC . Show that: (i)△ADC~△BEC (ii)CA×CE=CB×CD (iii)△ABC~△DEC (iv)CD×AB=CA×DE
View SolutionIn Fig. 4.170, ABCD is a trapezium in which AB∥DC and AB=2 DC . Determine the ratio of the areas of AOB and COD . (FIGURE)
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAB=750and ∠DBC=600. Compute ∠CDB and ∠ADB
View Solution

