In Figure, ABD is a triangle right-angled at A and AC⊥BD. Show that
(i)AB2=BC.BD
(ii) AC2=BC.DC
(iii) AD2=BD.CD
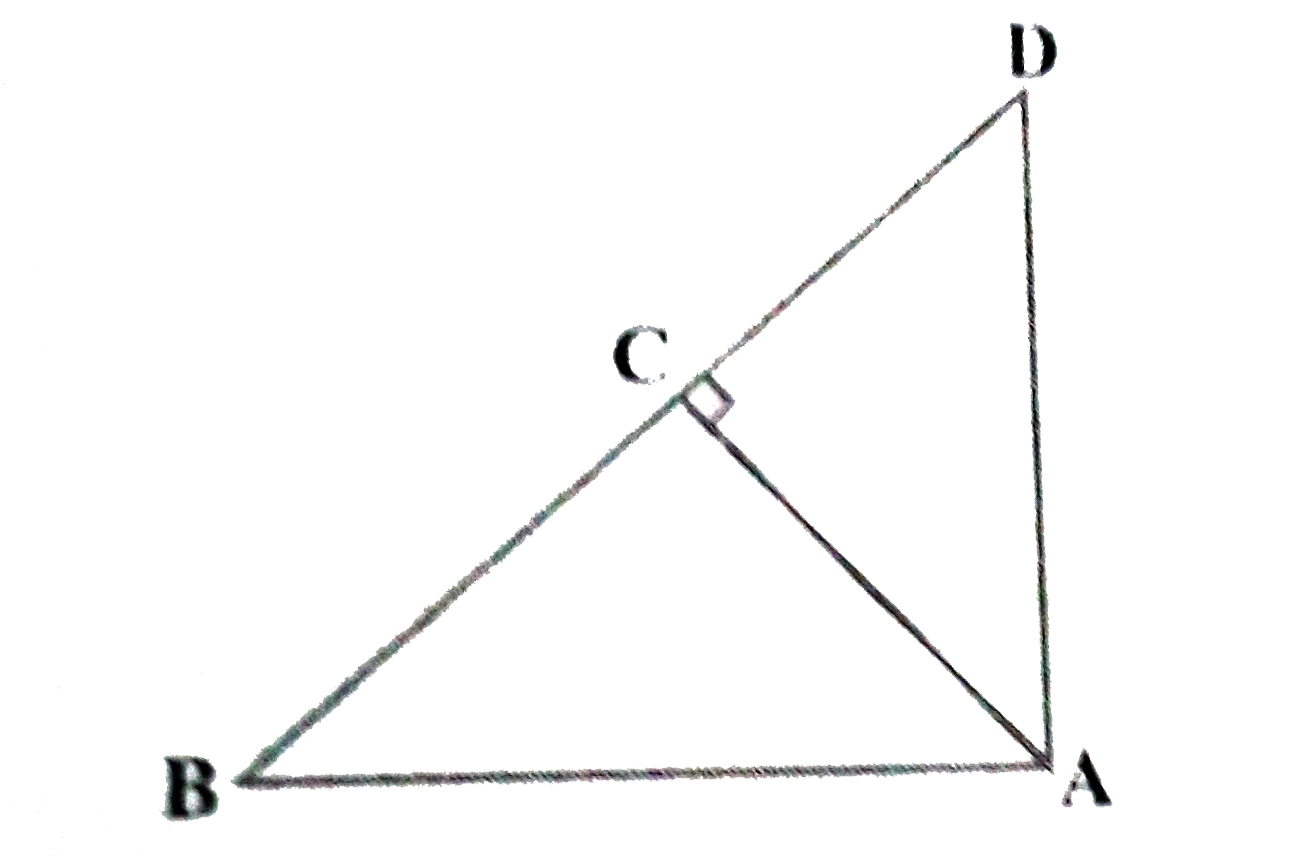
(##X06_E0503_s10##)
(i) Here, ABD is a triangle right angled at A and AC⊥BD
⇒ΔBAD∼ΔBCA
⇒ABBC=BDAB
(Corresponding sides of similar triangle)
⇒AB2=BC.BD
(ii) ABD is a triangle right angled at A and AC⊥BD
⇒ΔBCA∼ΔACD
⇒ACCD=BCAC
⇒(AC)2=(BC).(DC)(Corresponding sides of a similar triangle)
(iii) ABD is a triangle right angled at A and AC⊥BD
⇒ΔBAD∼ΔACD
⇒ADCD=BDAD
(AD)2=BD.CD(Corresponding sides of a similar triangle)
Similar Questions
ABD is a right triangle right-angled at A and AC⊥BD . Show that AB2=BC.BD (ii) AC2=BC.DC (iii) AD2=BD.CD (iv) AB2AC2=BDDC
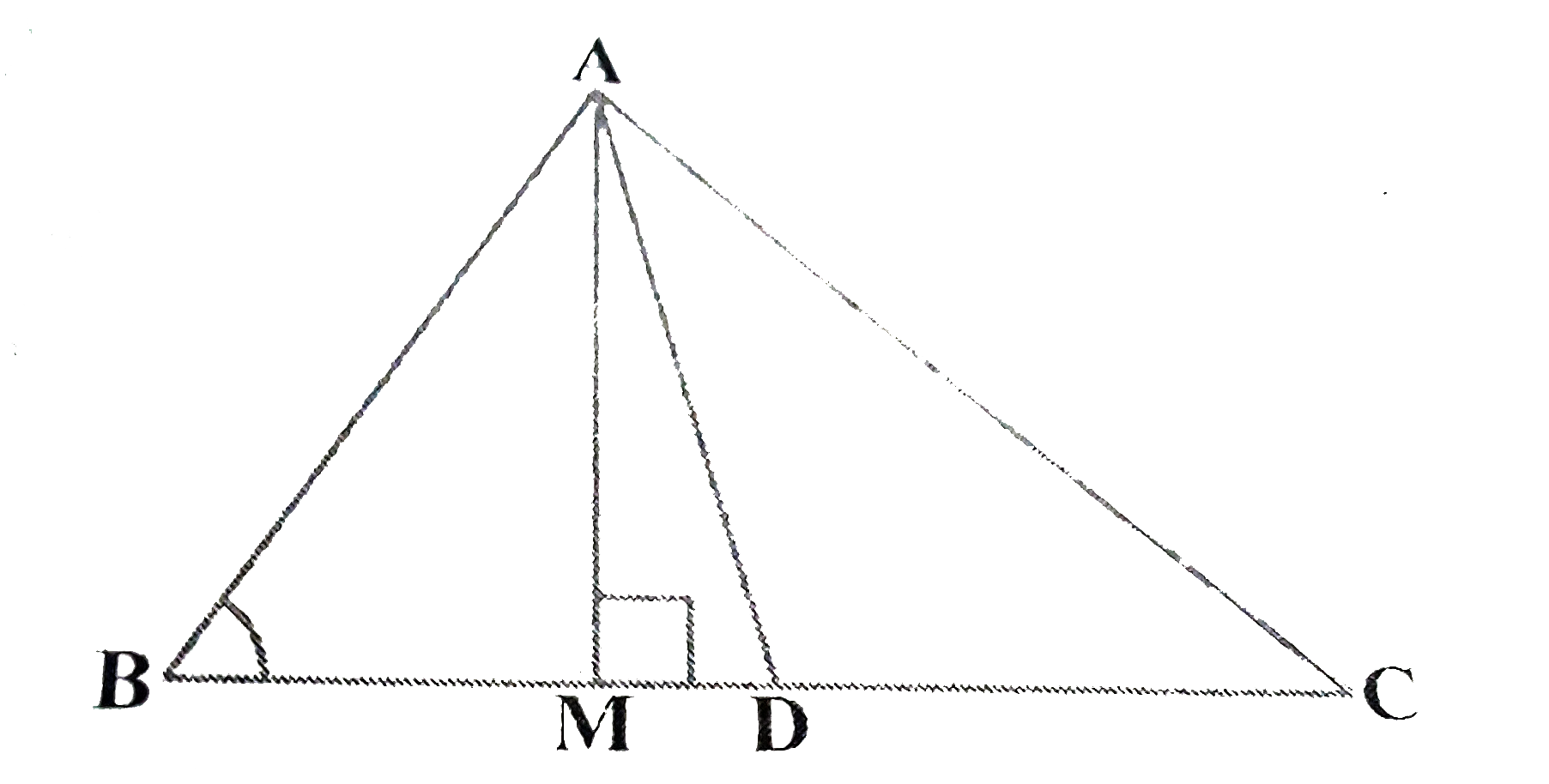
View SolutionIn figure, AD is a median of a triangle ABC and AM⊥BC. Prove that:
(i) AC2=AD2+BC.DM+(BC2)2
(ii) AB2=AD2−BC.DM+(BC2)2
(iii) AC2+AB2=2AD2+12BC2
View SolutionIn figure, ABC is a triangle in which ∠ABC=90∘and AD⊥BC. Prove that AC2=AB2+BC2−2BC.BD.

View SolutionIn figure, ABC is triangle in which ∠ABC>90∘ and AD⊥CBproduced. Prove that AC2=AB2+BC2+2BC.BD.

View SolutionIn Figure, ABC is an obtuse triangle, obtuse angled at B . If AD⊥CB , prove that AC2=AB2+BC2+2 BC×BD .
View SolutionIn Figure, ABCD is a trapezium in which AB∣∣CD and AD=BC. Show that :
(i) ∠A=∠B
(ii) ∠C=∠D
(iii) ABC≅BAD
(iv) diagonal AC=diagonalBD
View SolutionIn Figure, if ABC is an equilateral triangle. Find ∠BDC and ∠BEC
View SolutionIn Figure, ABC is a right triangle right angled at B and D is the foot of the the perpendicular drawn from B on AC . If DM⊥BC and DN⊥AB , prove that: (i)DM2=DN×MC (ii)DN2=DM×AN
View SolutionIn Figure, ABCD is a trapezium in which ABllCD and AD=BC. show that : ∠A=∠B (ii) ∠C=∠D (iii) A B C~= B A D(iv)DiagonalA C=diagnol B D
View SolutionABC is a right triangle right-angled at A and AD⊥BC . Then, BDDC= mm (a) (ABAC)2 (b) ABAC (c) (ABAD)2 (d) ABAD
View Solution
