In Figure, a crescent is formed by two circles which touch at A. C is the centre of the larger circle. The width of the crescent at BD is 9cm and at EF it is 5cm. Find (i) the radii of two circles (ii) the area of the shaded region.
Step by step video & image solution for In Figure, a crescent is formed by two circles which touch at A. C is the centre of the larger circle. The width of the crescent at BD is 9cm and at EF it is 5cm. Find (i) the radii of two circles (ii) the area of the shaded region. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
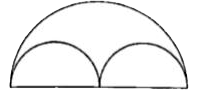
In the given figure there are 3 semicircles , the radii of each smaller circle is equal. If the radius of the larger circle be 22 cm , then the area of the shaded region is :
 A363π4B363π3C236.5πD363π
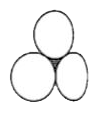
A363π4B363π3C236.5πD363πThree circle of equal radii touch each other as shown in figure . The radius of each circle is 1 cm. What is the area of shaded region ?
 A(2√3−π2)cm2B(3√2−π3)cm2C2√3πcm2Dnone of the above
A(2√3−π2)cm2B(3√2−π3)cm2C2√3πcm2Dnone of the above
In the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View SolutionIn the given figure two small circles touch each other externally at the centre of a big circle and these small circles are touched internally by a big circle of radius 74cm. Find the area of the shaded region

View SolutionIn the give figure, the sectors of two concentric circles of radii 7 cm and 3.5 cm are shown. Find the area of the shaded region.

View SolutionTwo circles touch internally. The sum of their areas is 116πcm2 and distance between their centres is 6 cm. Find the radii of the circles
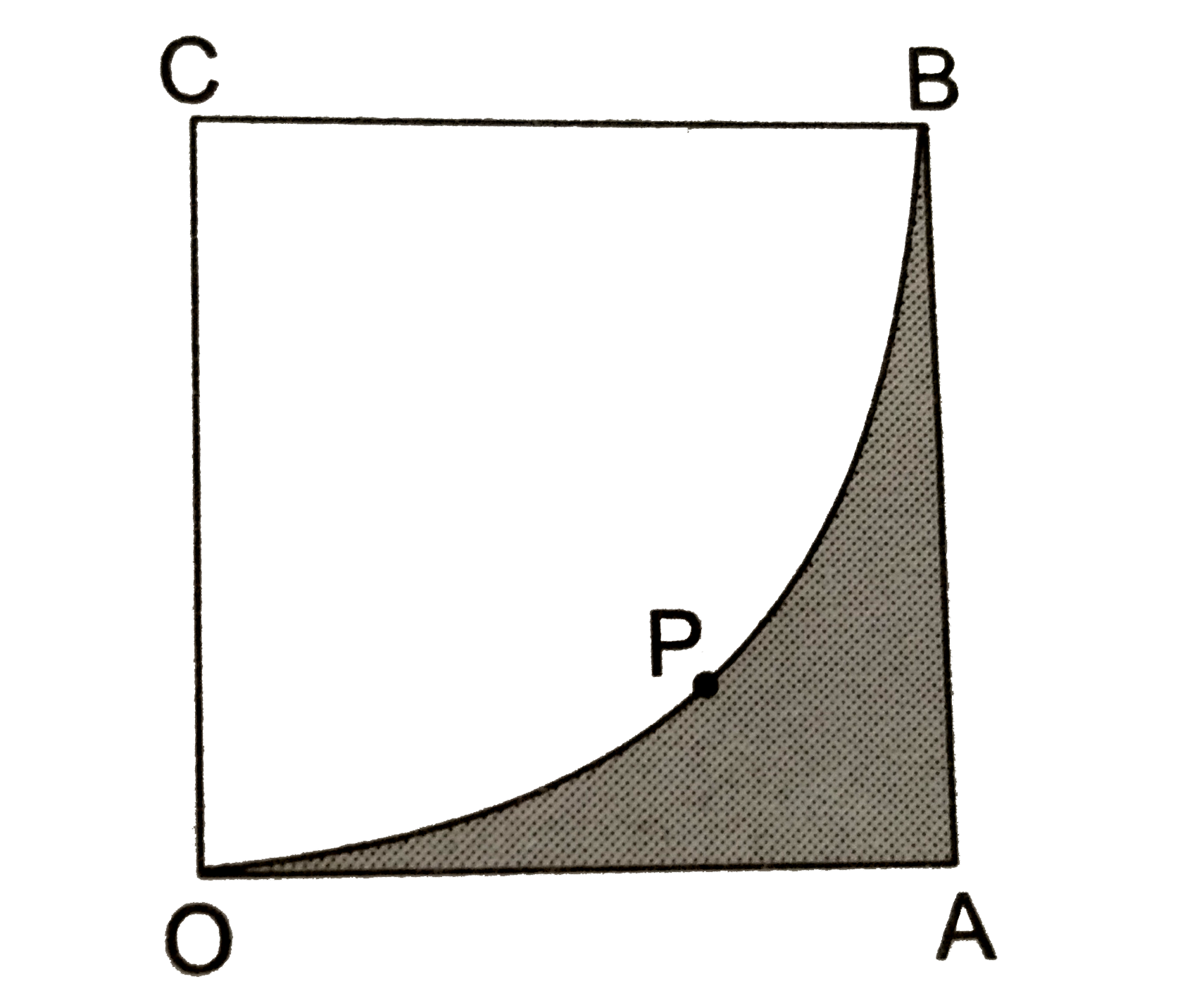
View SolutionIn the given figure, OABC is a square of side 7cm. If COPB is a quadrant of a circle with centre C find the area of the shaded region.
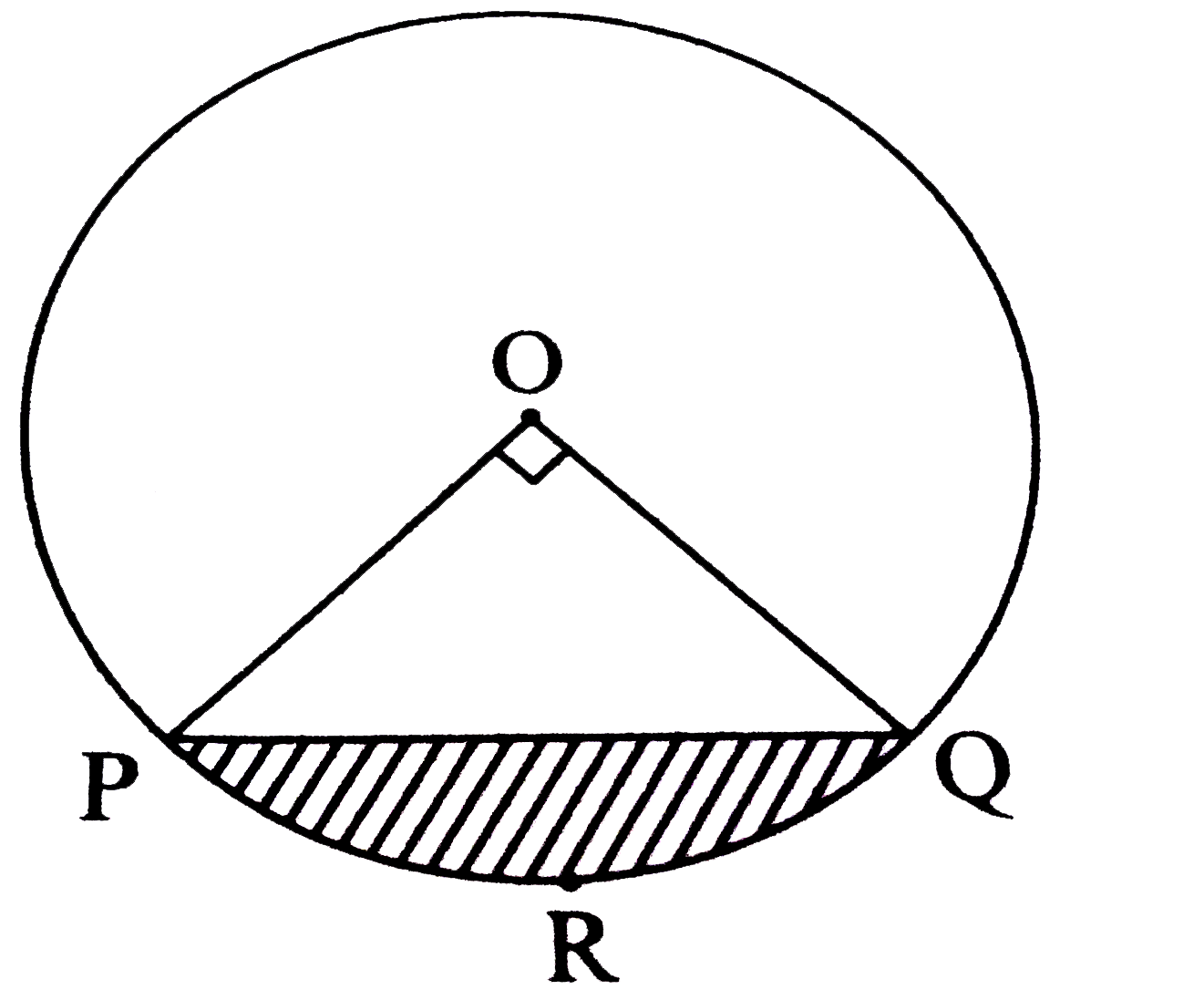
View SolutionIn the figure, if O is the centre of the circle, PQ is chord. ∠POQ=90∘ area of shaded region is 114cm2 find the radius of the circle
(π=3.14)
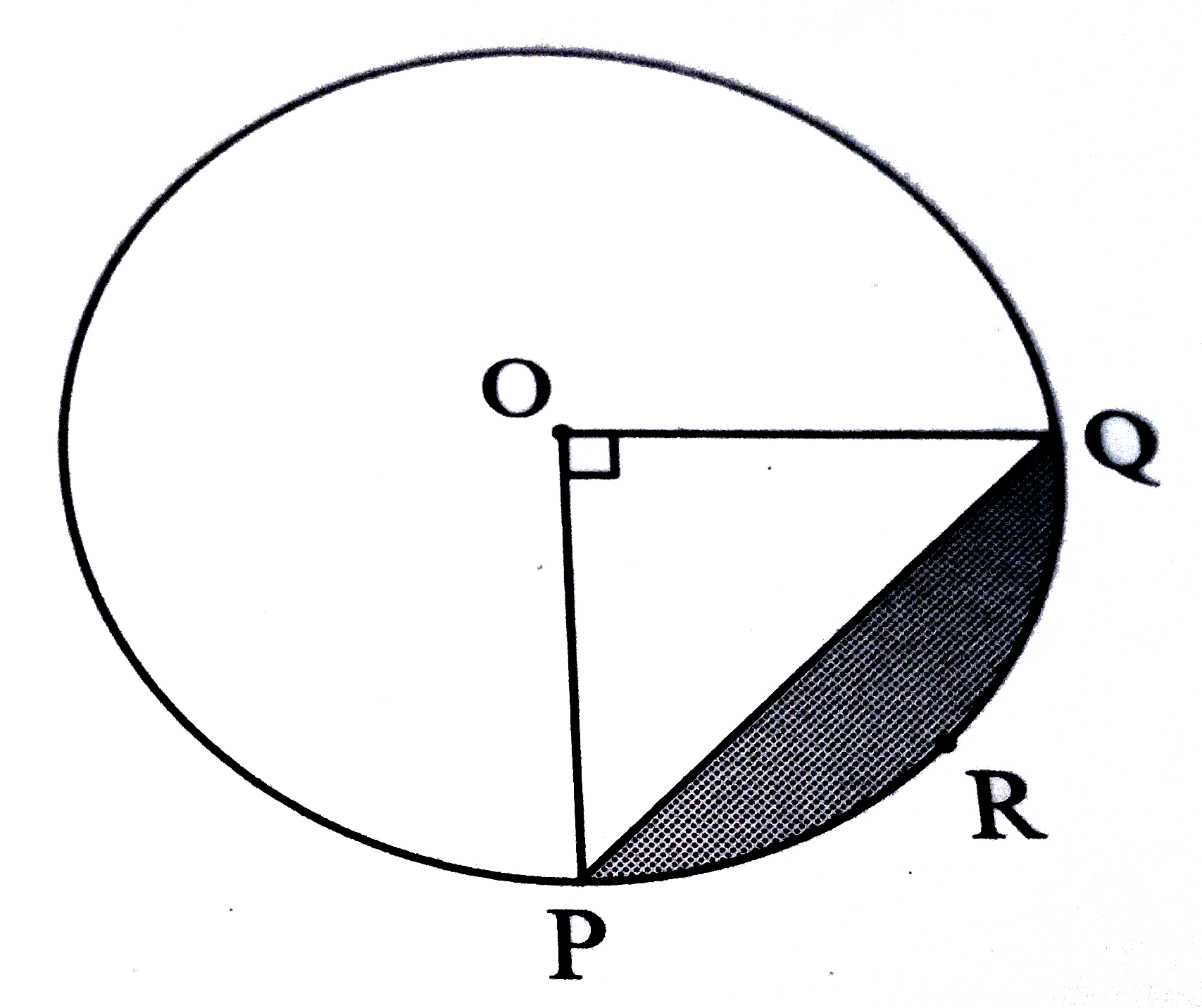
View Solution