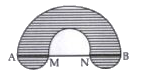
In Figure AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.
Let the radius of the circle be r.
and △PCM is right △
PC2=PM2+MC2
(9+r)2=(9)2+(16−r)2
81+r218r=81+324+r2−36r
54r=324
r=32454=6cm
Areaofshadedregion=324π2−81π+36π
=162π−117π
Therefore area of the shaded region =45πcm2
Topper's Solved these Questions
Similar Questions
In Figure AB = 36 cm and M is mid-point of AB. Semi-circles are drawn on AB, AM and MB as diameters. A circle with centre C touches all the three circles. Find the area of the shaded region.
View SolutionIn the figure, AB is a diameter of the circle with centre O and OA = 7cm. Find the area of the shaded region
View Solution
Knowledge Check
- Question 1 - Select One
AB is a line segment of length 48 cm and C is its mid-point. If three semicircles are drawn at AB, AC and CB using as diameters, then radius of the circle inscribed in the space enclosed by three semicircles is
A3√2B6C8D10
In the figure semicircles are drawn with PQ, PB and BQ as diameter. PB=BQ=21cm. A circle with centre O is drawn to touch all the three semicircles. Find its radius and also find the shaded region.
 View Solution
View SolutionABCD is a diameter of a circle of radius 6 cm such that AB = BC = CD. Semicircles are drawn on AB and BD as diameters, as shown in the given figure. Find the area of the shaded region.
 View Solution
View SolutionIn the given figure, AB and PQ are perpendicular diameters of the circle whose centre is O and radius OA = 7 cm. Find the area of the shade region.
 View Solution
View SolutionIn Fig. 12.25, ABCD is a square of side 14 cm. With centres A, B, C and D, four circles are drawn such that each circle touch externally two of the remaining three circles. Find the area of the shaded region.
View SolutionPS is the diameter of a circle of radius 6 cm. The points Q and R cts the diameter Ps. Semi circles are drawn on PQ and Qs as diameters. Find the area of the shaded region.
View SolutionIn the given figure, AB is the diameter of the largest semi-circle. AB = 21 cm, AM = MN = NB. Semi-circles are drawn with AM, MN and NB as shown. Using π=227, calculate the area of the shaded region.
 View Solution
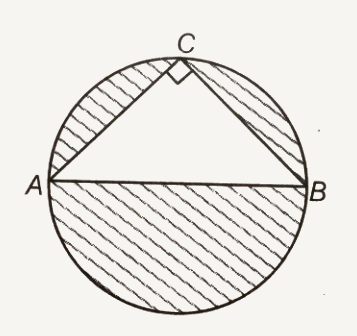
View SolutionIn figure , AB is a diameter of the circle, AC = 6cm and BC = 8cm . Find the area of the shaded region . (use π=3.14)
 View Solution
View Solution

