In figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
( c )
We know that the angle in a semicircle is 90∘.
∵ AOC is a diameter.
∴ ∠ABC=90∘
In △ABC
∠BAC+∠ABC+∠ACB=180∘
⇒ ∠BAC+90∘+50∘=180∘ ⇒ ∠BAC=180∘−140∘=40∘
Now AT is the tangent.
∴ ∠OAT=90∘
⇒ ∠OAB−∠BAT=90∘
⇒ ∠BAT=90∘−∠BAC=90∘−40∘=50∘
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise25videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question7videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions3videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions9videos
CO-ORDINATE GEOMETRY
Similar Questions
In the given figure A,B is a chord of the circle and AOC is its diameter ,such that ∠ACB=50∘ .If AT is the tangent to the circle at the point A, then ∠BAT is equal to :
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
View Solution
Knowledge Check
- Question 1 - Select One
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
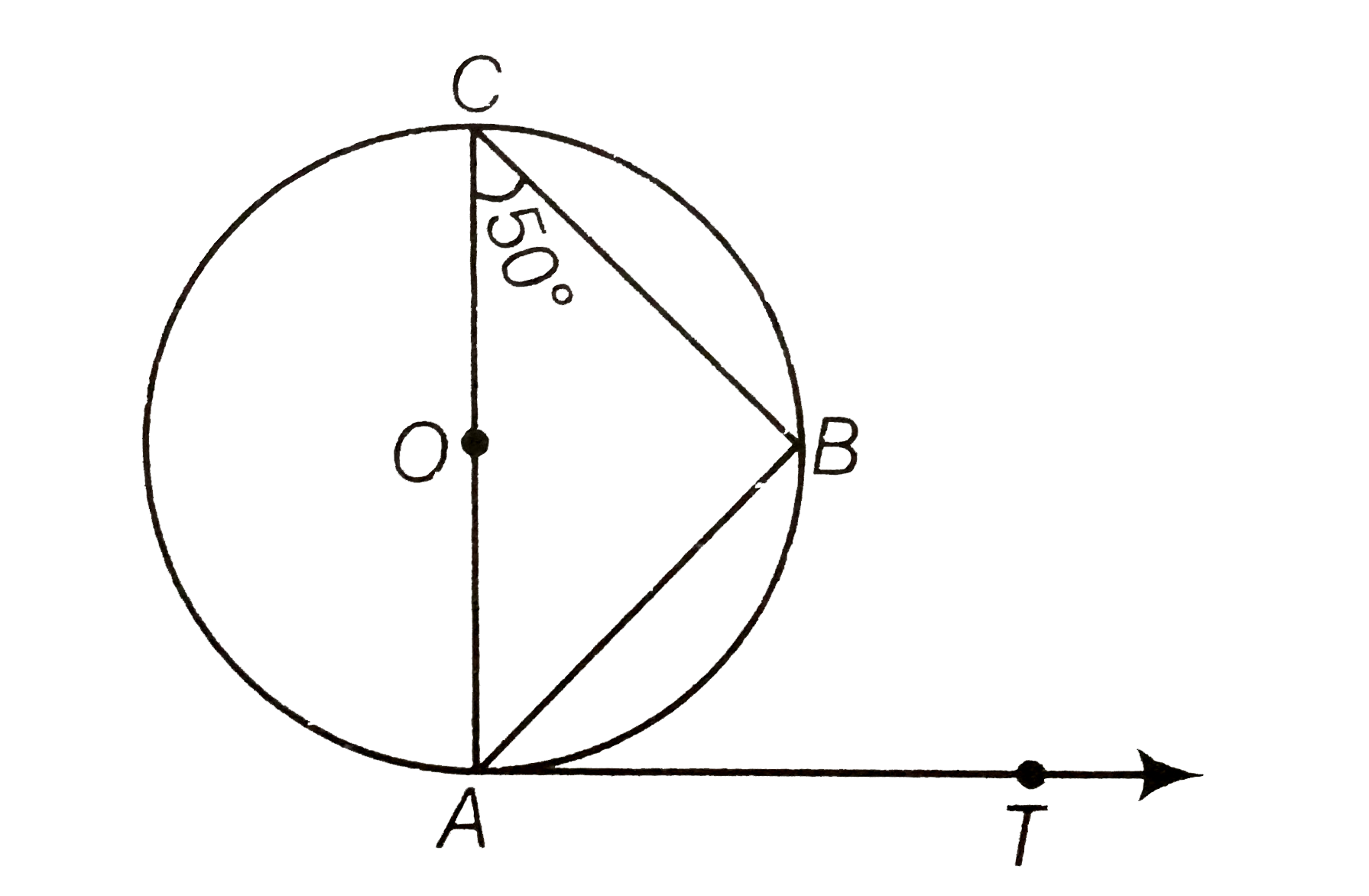A45∘B60∘C50∘D55∘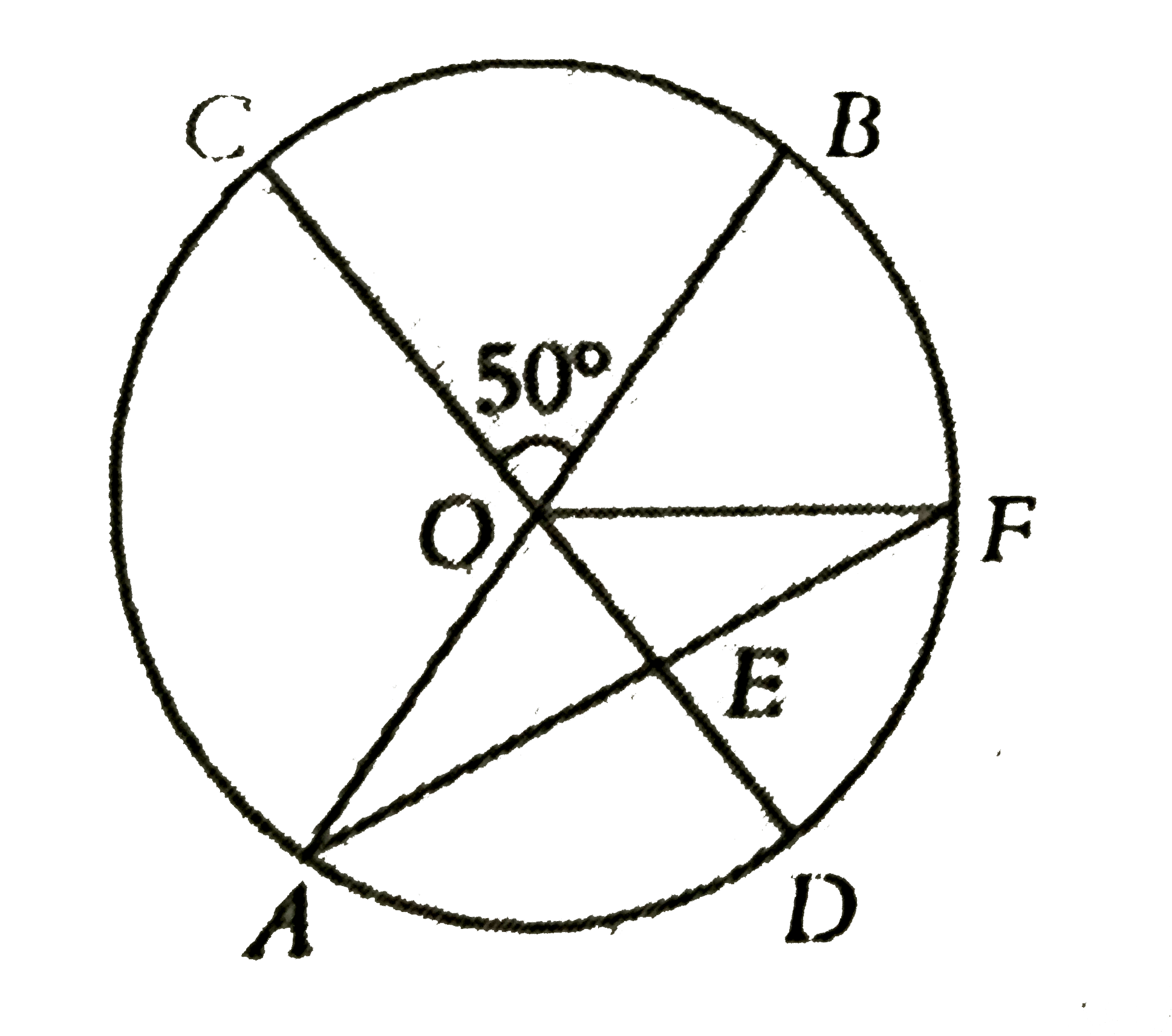 - Question 2 - Select One
In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADFA130∘B100∘C110∘D120∘ - Question 3 - Select One
AB is a chord to a circle and PAT is the tangent to the circle at A. If ∠BAT=75∘and∠BAC=45∘, C being a point on the circle, then ∠ABC is equal to
A40∘B45∘C60∘D70∘
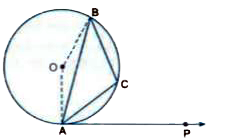
In fig AB is chord of a circle with centre O and AP is the tangent at A such that ∠BAP=75∘ find ∠ACB
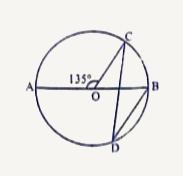
View SolutionIn the figure, AB is the diameter of the circle. If ∠AOC=135∘ then find the ∠CDB.
View SolutionIn Figure-2 PQ is tangent to the circle with centre at O , at the point B. If ∠AOB = 100∘ , then ∠ABP is equal to
(A) 50∘
(B) 40∘
(C) 60∘
(D) 80∘View Solution-
In the above figure , O is the centre of the circle, AB and CD are diameters. ∠COB=50∘=50∘ . If E is the midpoint of AF, then find ∠ADFView Solution In the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
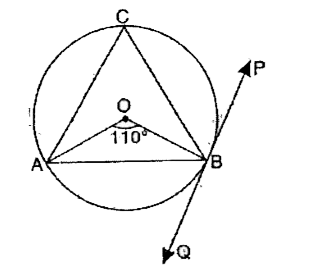
View Solution