AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
True.
CD is a tangent at contact point C. AOB is diameter which meets tangent produced at D.
Chord AC makes ∠A=30∘ with diameter AB.
To Prove : BD−BC
Proof : In △OAC,
OA=OC=r (radii of same dircle)
∠1=∠A (angles opposite to equal sides are equal)
⇒ ∠1=30∘ (∵∠A=30∘)
Exterior ∠BOC=∠2=∠1+∠A=(30∘+30∘)=60∘
Now, in △OCB,
OB=OC (radii of same circle)
∴ ∠3=∠4 (angles opposite to equal sides are equal)
∠3+∠4+∠COB=180∘
⇒ ∠3+∠3+60∘=180∘ (angle sum property of triangle)
⇒ 2∠3=180∘−60∘=120∘
⇒ ∠3=60∘=∠4
⇒ ∠6+∠4=180∘ (linear pair axiom)
⇒ ∠6=180∘−∠4=180∘−60∘
⇒ ∠6=120∘
∴ Tangent CD and radius CO are at contact point C.
∴ ∠OCD=90∘
(radius through point of contact is perpendicular to the tangent )
⇒ ∠3+∠5=90∘ ⇒ 60∘+∠5=90∘
⇒ ∠5=30∘
Now, in △BCD,
∴ ∠5+∠6+∠D=180∘ (angle sum property)
⇒ 120∘+30∘+∠D=180∘ ⇒ ∠D=30∘
Since, ∠C=∠D=30∘.
Hence, BC=BD (sides opposite to equal angles)
 Hence Proved.
Hence Proved.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Exercise25videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Very Short Answer Question7videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLESEXERCISE - Revision Exercise Long Answer Questions3videos
CIRCLES
- BOOK - NAGEEN PRAKASHANCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Revision Exercise Long Answer Question5videos
ARITHMETIC PROGRESSION
- BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRYEXERCISE - Revision Exercise Short Answer Questions9videos
CO-ORDINATE GEOMETRY
Similar Questions
AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View Solution
Knowledge Check
- Question 1 - Select One
In figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
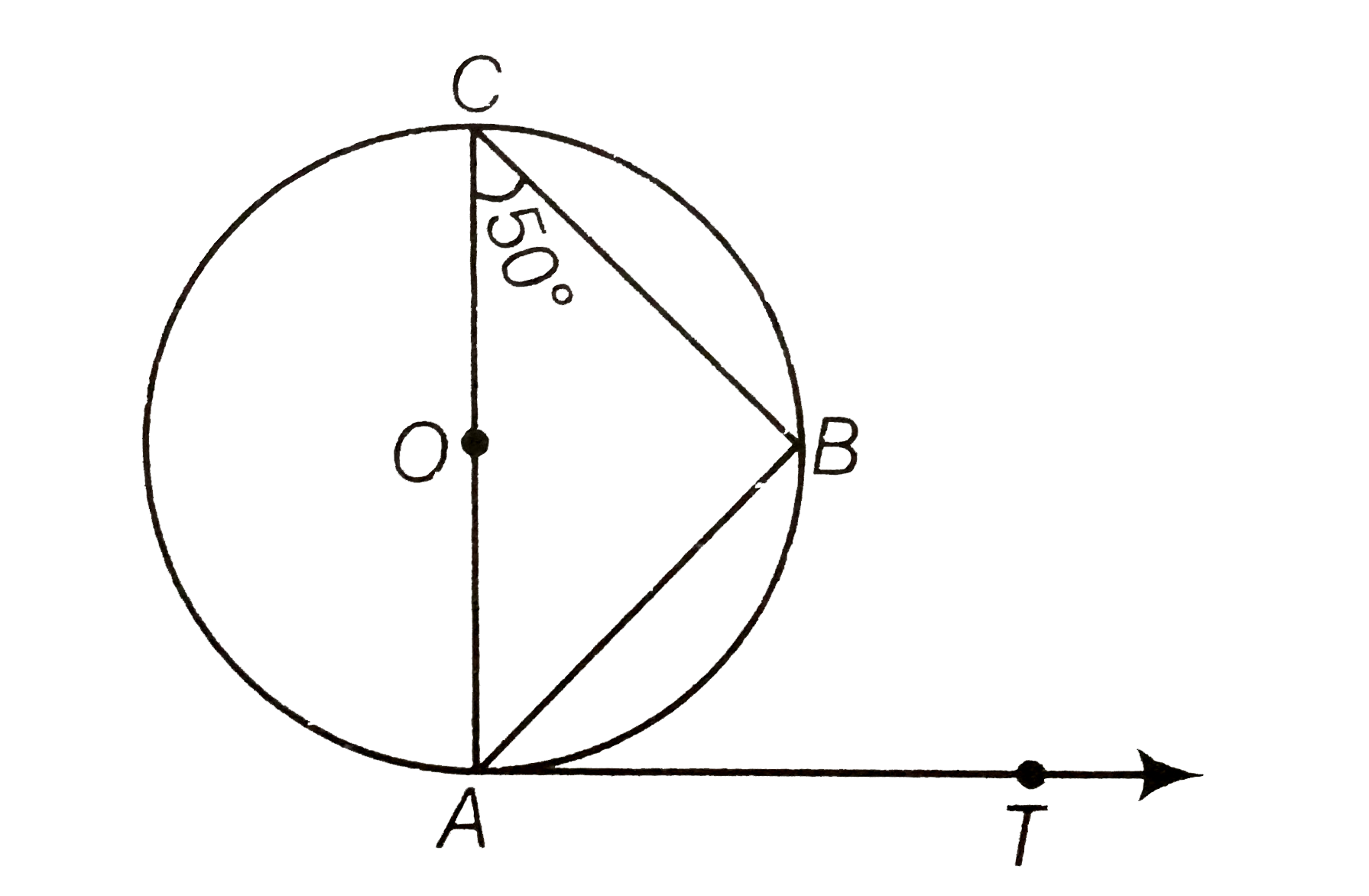 A45∘B60∘C50∘D55∘
A45∘B60∘C50∘D55∘ - Question 2 - Select One
AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Find the ∠AEB.
A30∘B60∘C90∘D45∘
AB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD = AB. The tangent at B meets the line AC produced at E then AE is equal to
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionSeg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
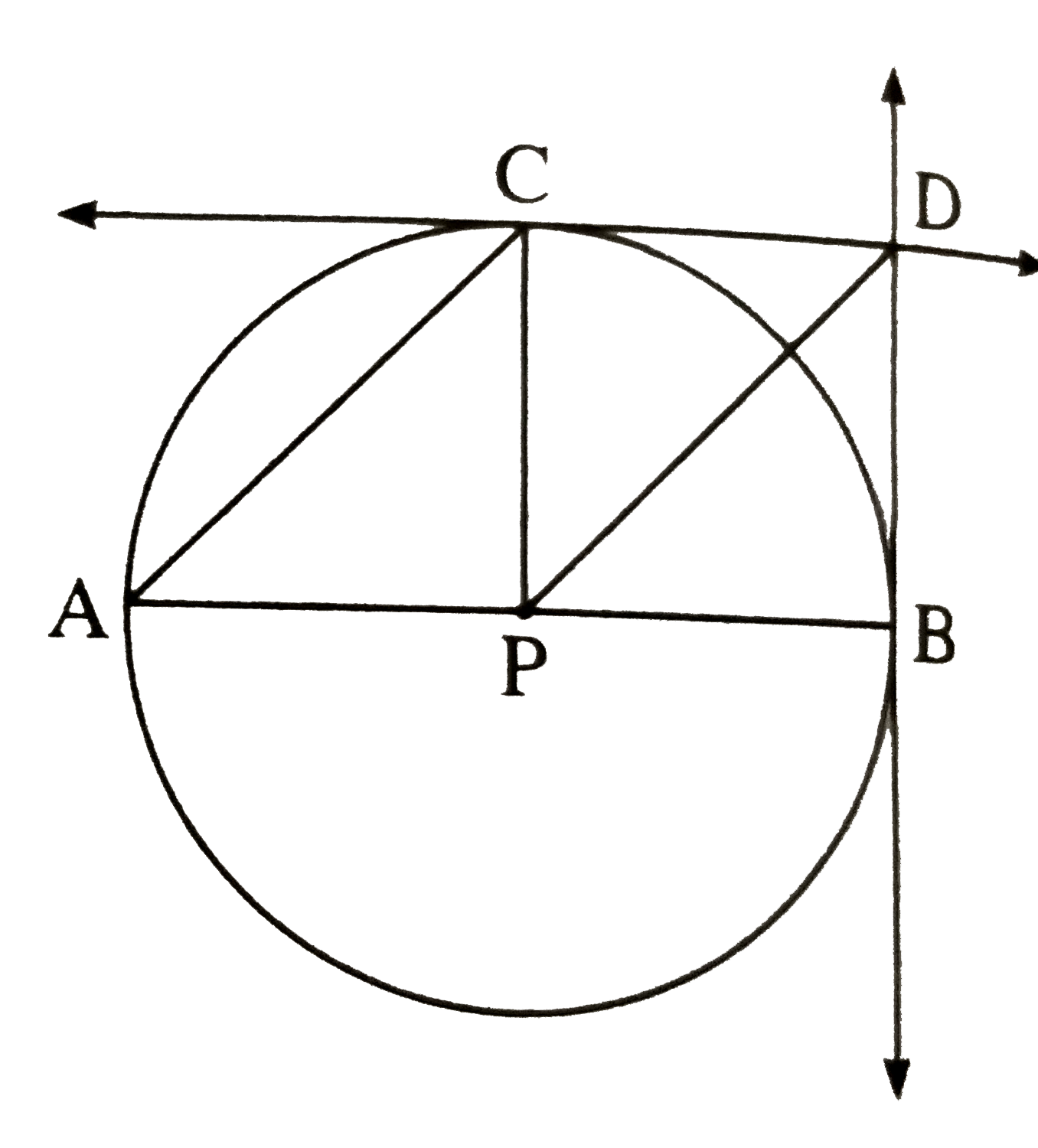 View Solution
View SolutionAB is diameter of a circle with centre 'O'. CD is a chord which is equal to the radius of the circle. AC and BD are extended so that they intersect each other at point P. Then find the value of ∠APB.
View SolutionAB is the diameter of a circle whose centre is O. DC is a chord of that circle. If DC||AB and ∠BAC=20∘ then ∠ADC=?
View Solution

