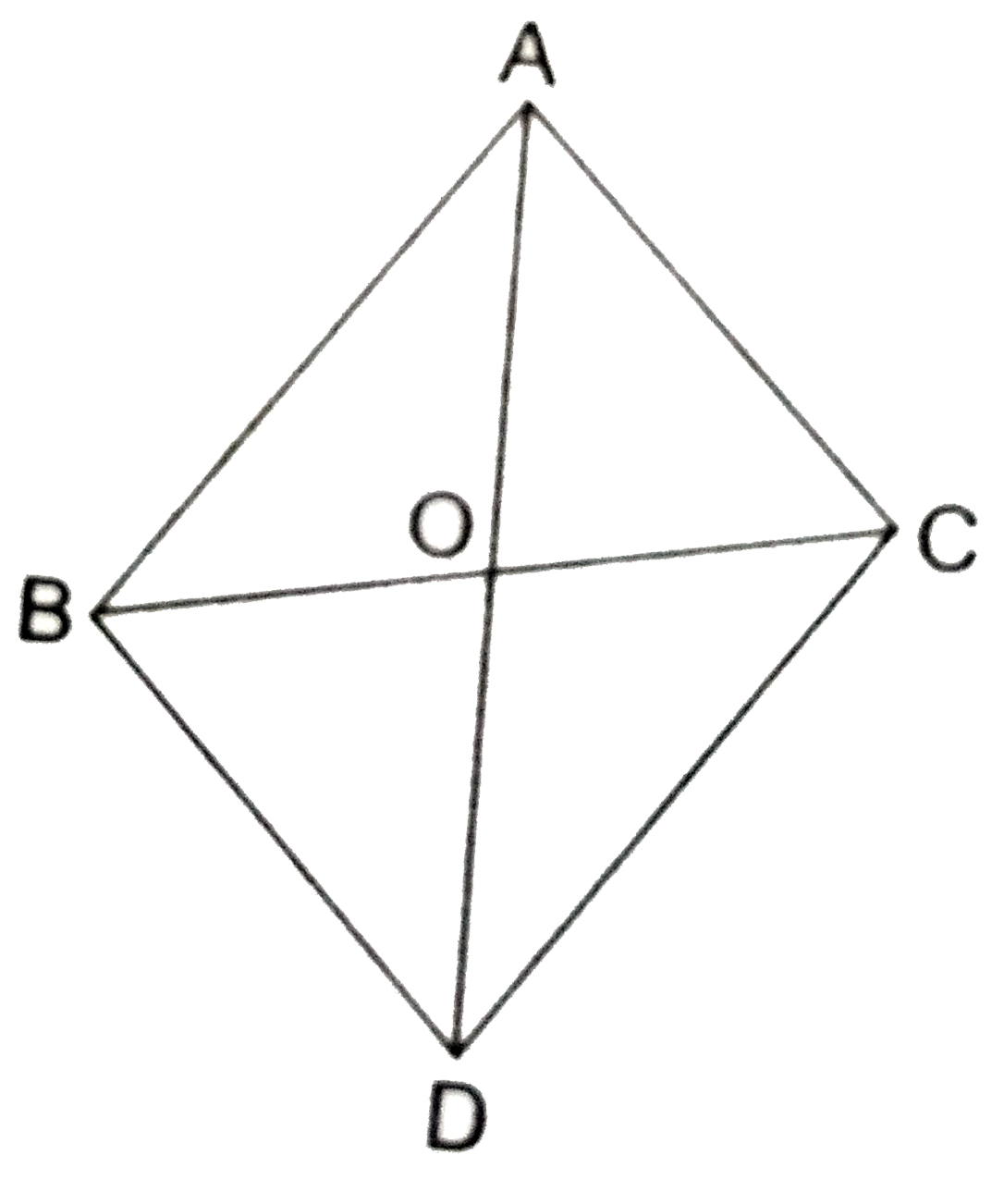
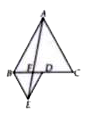
In figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.
Step by step video solution for In figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that (a r(A B C))/(a r(D B C))=(A O)/(D O). by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SELF ASSESSMENT 11EXERCISE - Section (iii)8videos
SAMPLE PAPER SELF ASSESSMENT 11
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 9 (SELF-ASSESSMENT)EXERCISE - Section-C (Case Study Based Questions)10videos
SAMPLE PAPER 9 (SELF-ASSESSMENT)
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER SOLVED 10EXERCISE - PART - B ( SECTION - V )5videos
SAMPLE PAPER SOLVED 10
Similar Questions
In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
 View Solution
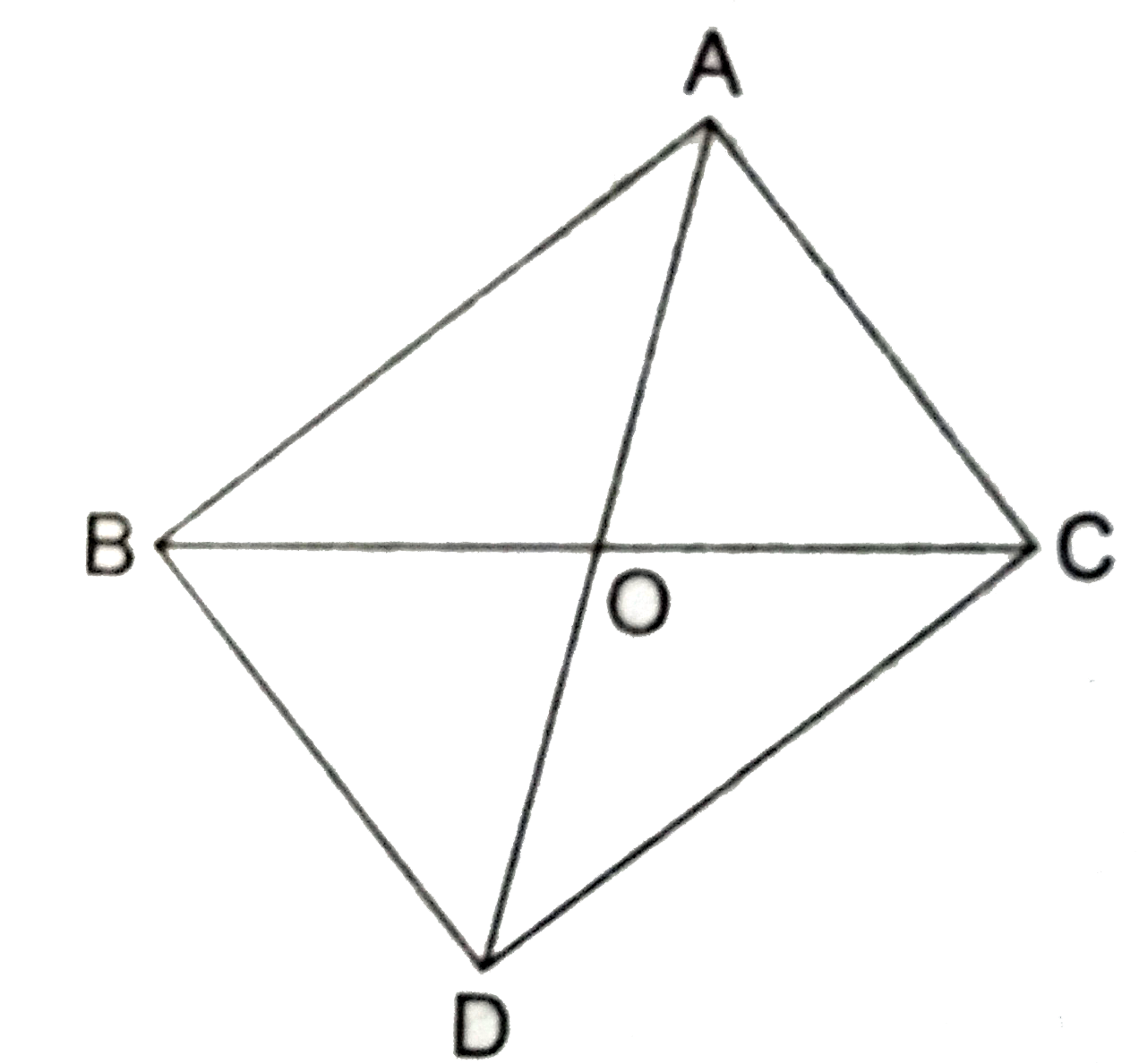
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
 View Solution
View SolutionIn Fig. 4.179, ABC and DBC are on the same base BC . If AD and BC intersect at O , prove that Area (ABC)Area (DBC)=AODO (FIGURE)
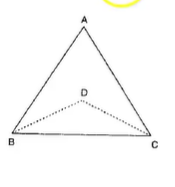
View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
 View Solution
View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
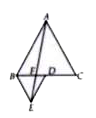
ar(ΔBDE) = 1/4 ar(ΔABC)View SolutionIn figure, ABC and BDE are two equilateral triangles such that D is the mid-point of BC. If AE intersects BC at F, show that
ar(ΔABC) = 2 ar(ΔBEC)View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD
 View Solution
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
 View Solution
View Solution

