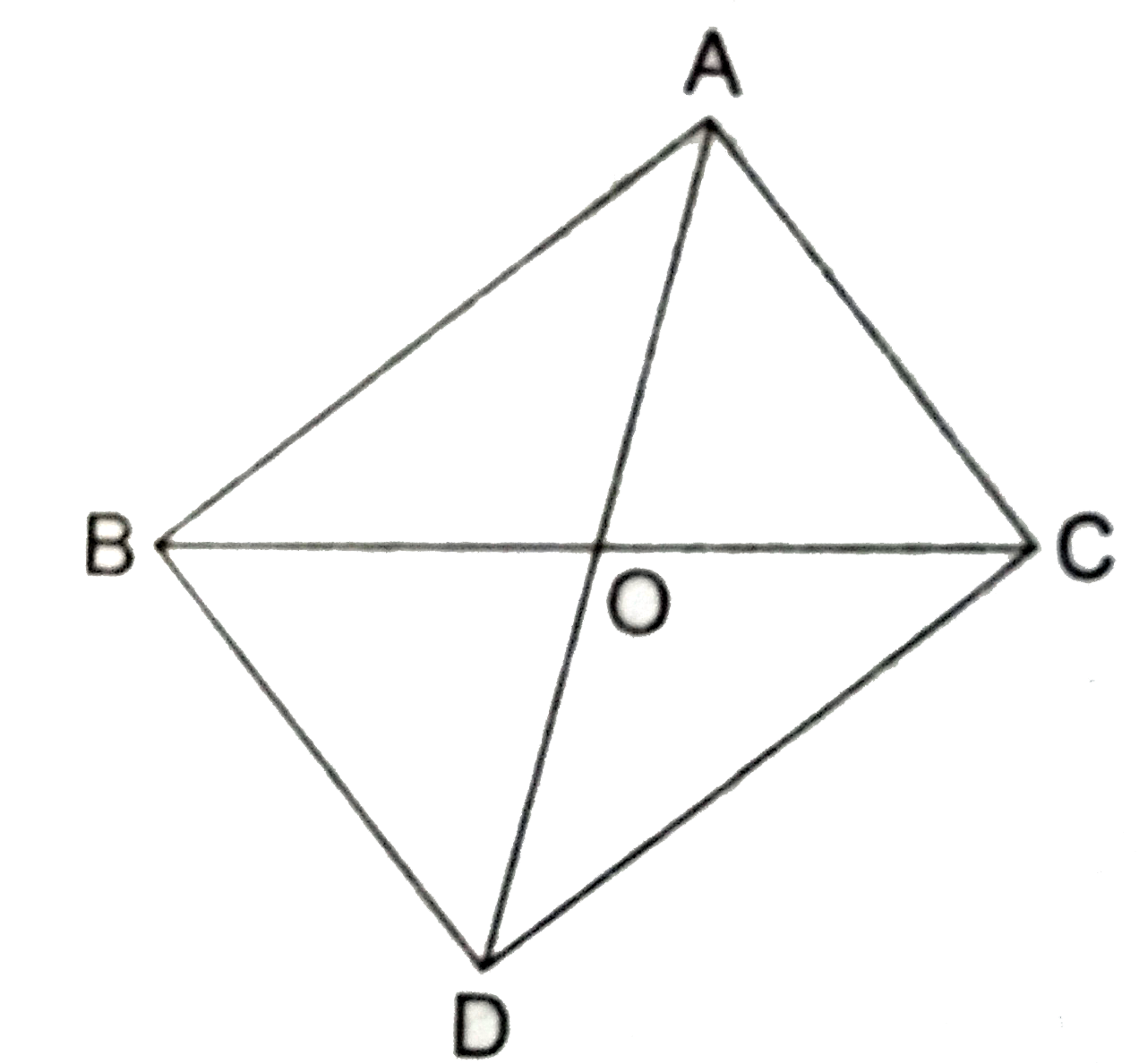
In Fig. 6.44, ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)= AODO
Consider ∠AOM and∠DNO
∠AOM=∠DON(oppesite angles)
∠AMO=∠DNO=90∘
∠AOM≅∠DNO
ar(∠AOM)ar(∠DNO)=(AM)2(DN)2=(AO)2(DO)2
Ratio of the area of similar triangles is equal too the square of their corresponding sides.
(AM)2(DN)2=(AO)2(DO)2
AMDN=AODO−(1)
ar(∠ABC)ar(∠DBC)=12⋅b⋅h12⋅b⋅h
=12⋅BC⋅AM12⋅BC⋅DN
=AMDN
from equation 1
ar(∠ABC)ar(∠DBC)=AODO
Hence proved.
Similar Questions
In figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View SolutionIn figure ABC and DBC are two triangles on the same base BC. If AD intersects BC at O, show that ar(ABC)ar(DBC)=AODO.

View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
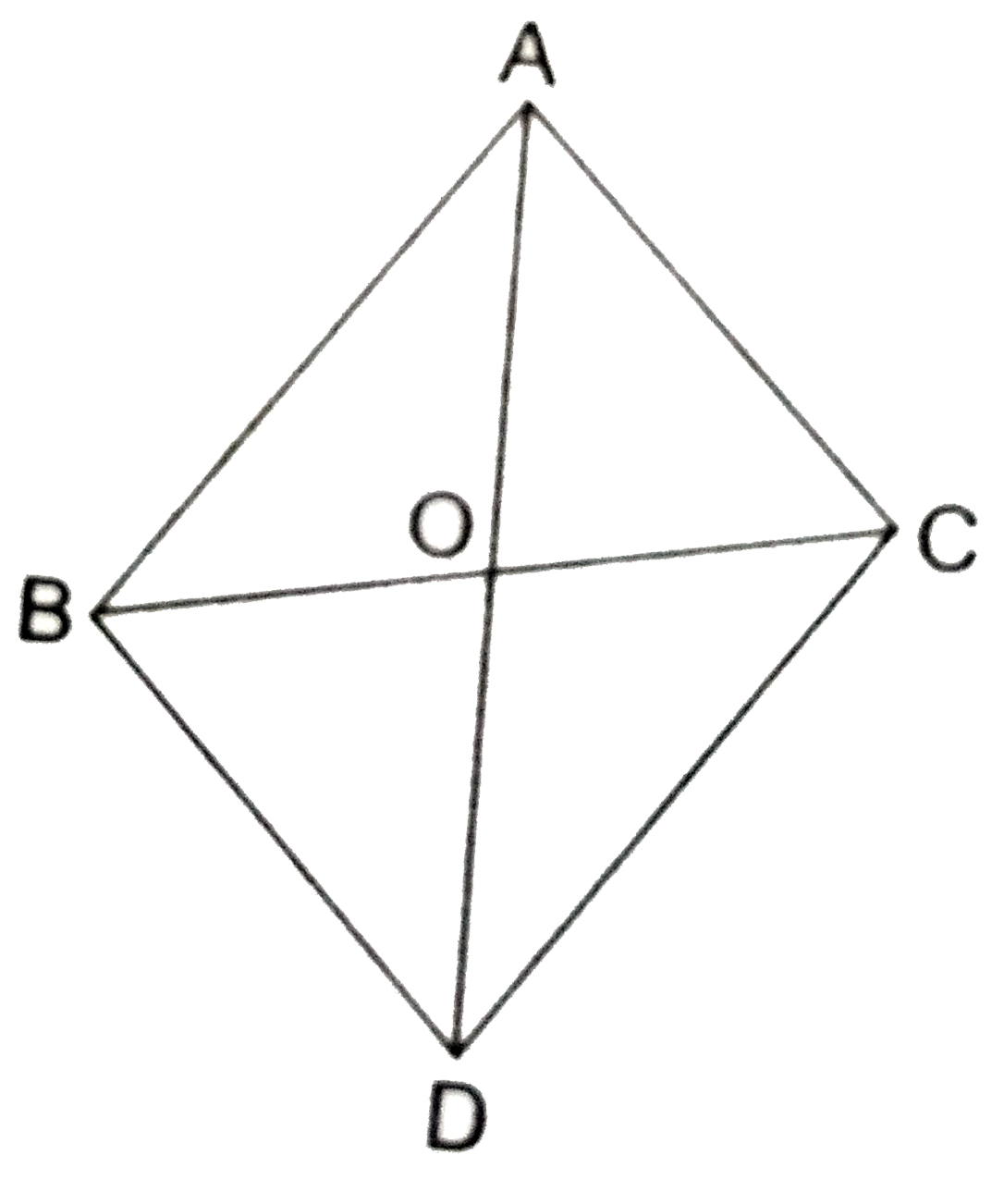
View SolutionIn Figure, ABC and DBC are two triangles on the same base BC such that AB=AC and DB=DC. Prove that ∠ABD=∠ACD
View SolutionIn the given figure, ΔABCandΔDBC have the same base BC. If AD and BC intersect at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
View Solution△ABCand△DBC are two triangles on the same base BC. A and D lies on opposite sides of BC. Prove that ar(△ABC)ar(△DBC)=AODO
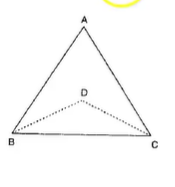
View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD

View SolutionABC and DBC are two isosceles triangles on the same base BC (see Fig. 7.33). Show that∠ABD =∠ACD

View Solution