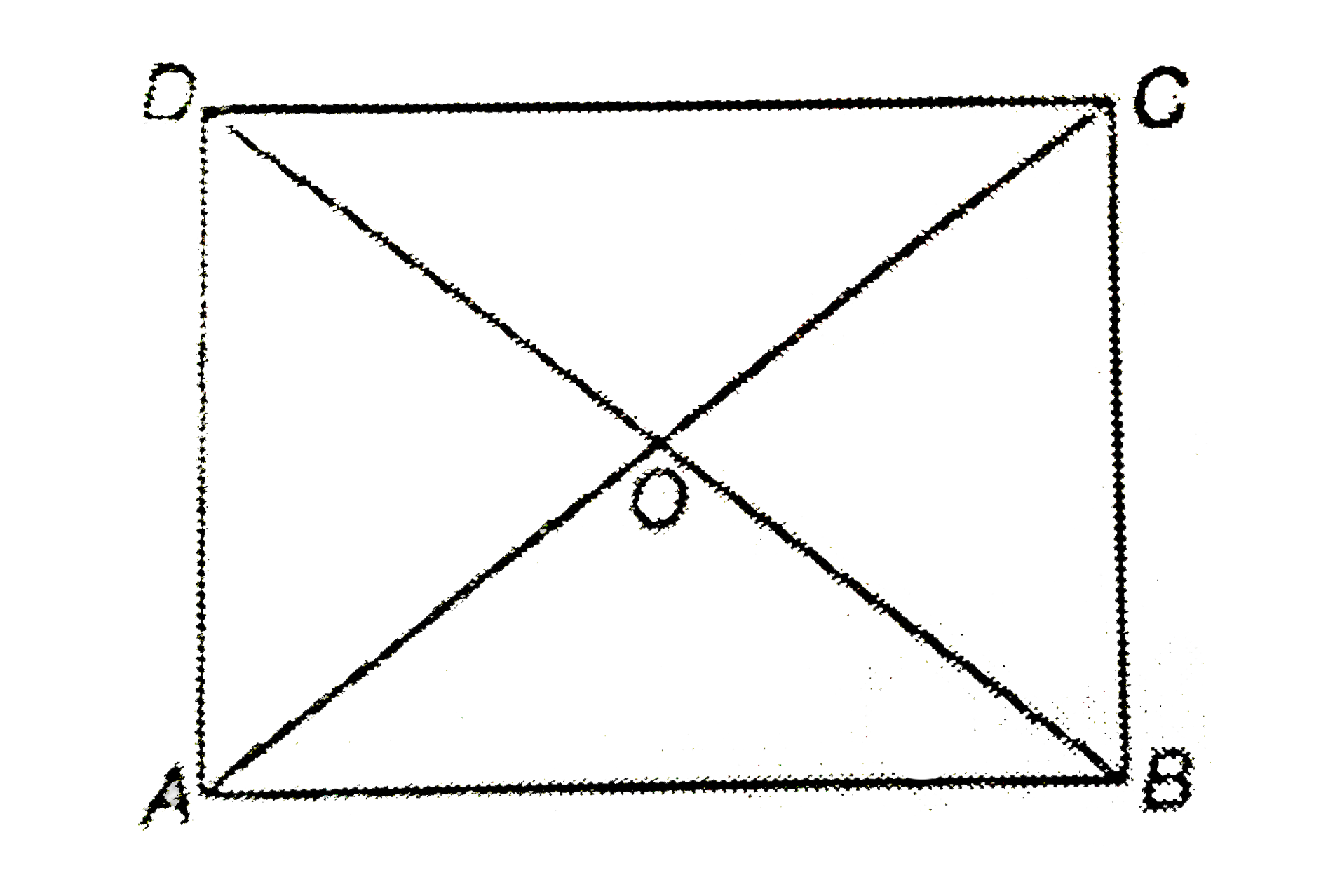
In figure, ∠B<∠A and ∠C<∠D. Show that AD<BC.
To solve the problem, we need to show that if ∠B<∠A and ∠C<∠D, then AD<BC. Here’s a step-by-step solution:
Step 1: Understand the Angles and Sides
Given:
- ∠B<∠A
- ∠C<∠D
From the properties of triangles, we know that the side opposite a larger angle is longer than the side opposite a smaller angle.
Step 2: Relate Angles to Their Opposite Sides
From ∠B<∠A:
- The side opposite ∠B is AO.
- The side opposite ∠A is BO.
- Therefore, we can conclude that:
AO<BO
From ∠C<∠D:
- The side opposite ∠C is OD.
- The side opposite ∠D is OC.
- Therefore, we can conclude that:
OD<OC
Step 3: Combine the Inequalities
Now we have two inequalities:
1. AO<BO
2. OD<OC
Step 4: Add the Inequalities
By adding the two inequalities:
AO+OD<BO+OC
Step 5: Substitute the Sides
Now, we can substitute:
- AO+OD is equal to AD
- BO+OC is equal to BC
Thus, we can rewrite the inequality as:
AD<BC
Conclusion
We have shown that if ∠B<∠A and ∠C<∠D, then AD<BC.
Given:
- ∠B<∠A
- ∠C<∠D
From ∠B<∠A:
- The side opposite ∠B is AO.
- The side opposite ∠A is BO.
- Therefore, we can conclude that:
AO<BO
- The side opposite ∠C is OD.
- The side opposite ∠D is OC.
- Therefore, we can conclude that:
OD<OC
Now we have two inequalities:
1. AO<BO
2. OD<OC
By adding the two inequalities:
AO+OD<BO+OC
Now, we can substitute:
- AO+OD is equal to AD
- BO+OC is equal to BC
AD<BC
We have shown that if ∠B<∠A and ∠C<∠D, then AD<BC.
Topper's Solved these Questions
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Problems From NCERT/exemplar
5 Videos
- TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIANGLESEXERCISE - Exercise 7a
35 Videos
- SURFACE AREA AND VOLUMEBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - SURFACE AREA AND VOLUMEEXERCISE - Revision Exercise (long Answer Questions)
10 Videos
Similar Questions
Find ∠A+∠B+∠C+∠D
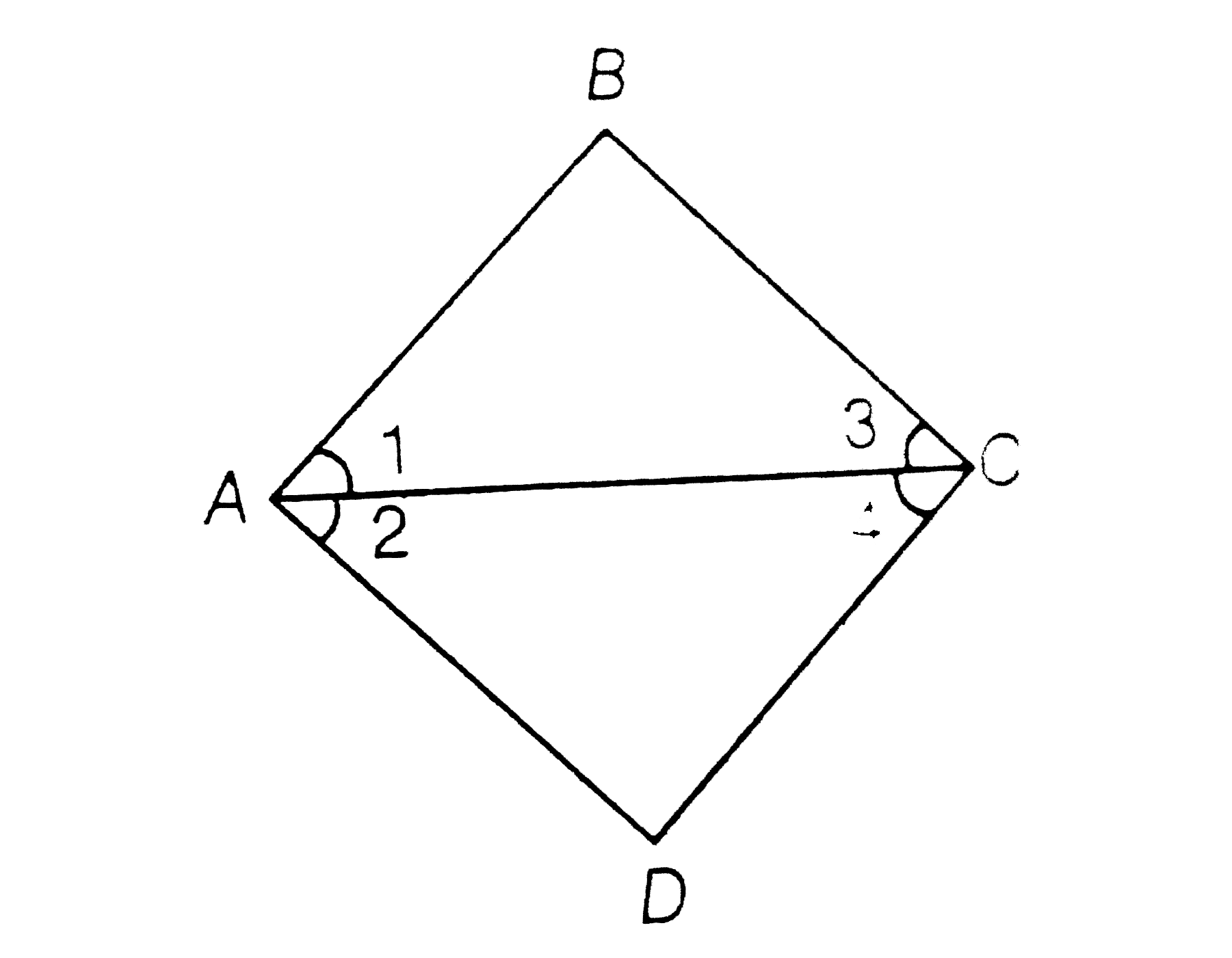
View SolutionIn the adjoining figure, we have ∠1=∠3and∠2=∠4. Show that ∠A=∠C.
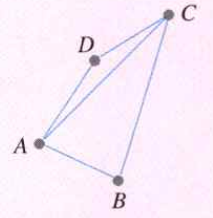
View SolutionIn the adjoining figure, AB>AC and the angle bisectors of ∠B and ∠C meet at point P. Prove that
PB>PC.

View SolutionABCD is a rectangle in which diagonal AC bisects ∠A as well as ∠C. Show that
(i) ABCD is a square
(ii) diagonal BD bisects ∠B
View SolutionIn the figure if AB || CD and AD||BC, find ∠Aand∠D
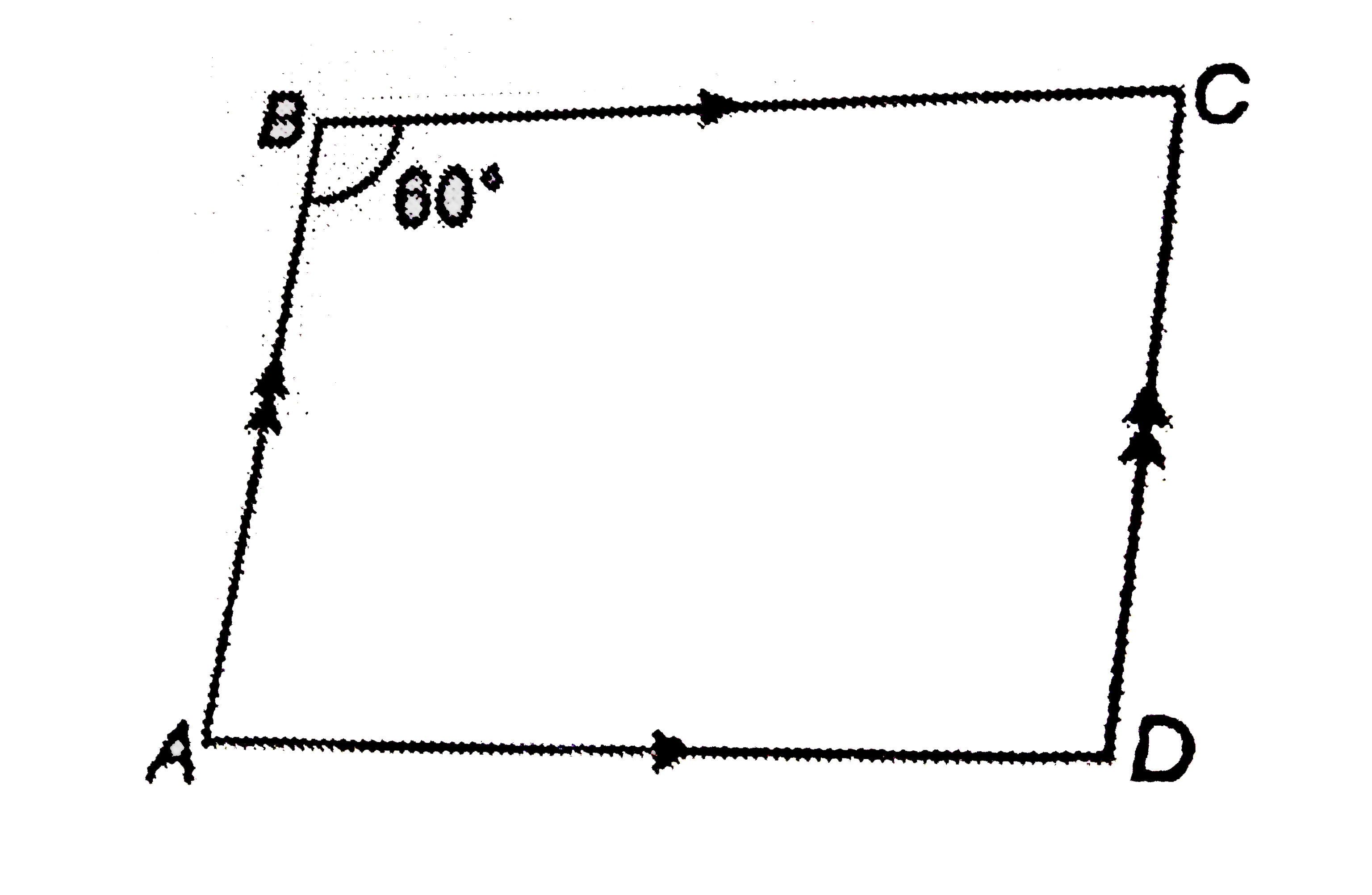
View SolutionIf bisectors of ∠Aand∠B of a quadrilateral ABCD intersect each other at P, of ∠Band∠C at Q, of ∠Cand∠D of R and of ∠Dand∠A at S, then PQRS is a (A) Rectangle (B) Rhombus (C) Parallelogram (D) Quadrilateral whose opposite angles are supplementary
View SolutionFind ∠A+∠B+∠C+∠P+∠Q+∠R.

View SolutionGiven the base BC of the triangle ABC and if ∠C−∠B=k, a constant, show that the locus of the vertex A is a hyperbola.
View SolutionIf A, B and C are angles of a triangle such that ∠A is obtuse, then show tan B tanC<1.
View SolutionIn a quadrilateral ABCD the linesegment bisecting ∠Cand∠D meet at E. Prove that ∠A+∠B=2∠CED.
View Solution
