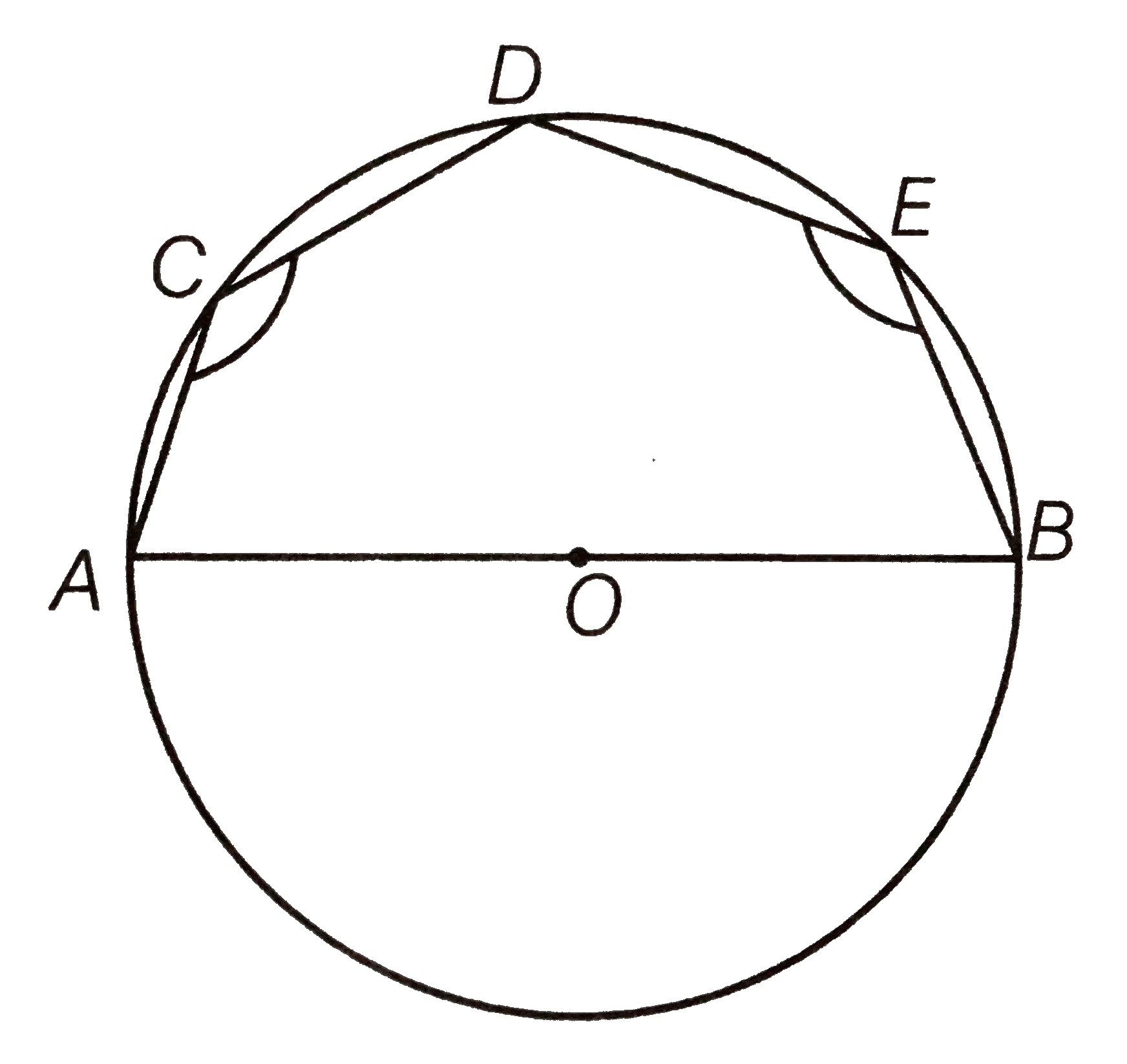
In figure, AOB is a diameter of the circle and C, D, E are any three points on the semi-circle. Find the value of ∠ACD+∠BED.
Video Solution
Text Solution
In the given figure, join AE.
Since, A, C, D and E are four point on a circle, then ACDE is a cyclic quadrilateral.
∴∠ACD+∠AED=180∘ …(i)
[sum of opposite angles in a cyclic quadrilateral is 180∘]
Now, ∠AEB=90∘...(ii)
We know that, diameter subtends a right angle to the circle.

On adding Eqs. (i) and (ii), we get
(∠ACD+∠AED)+∠AEB=180∘+90∘=270∘
⇒∠ACD+∠BED=270∘
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
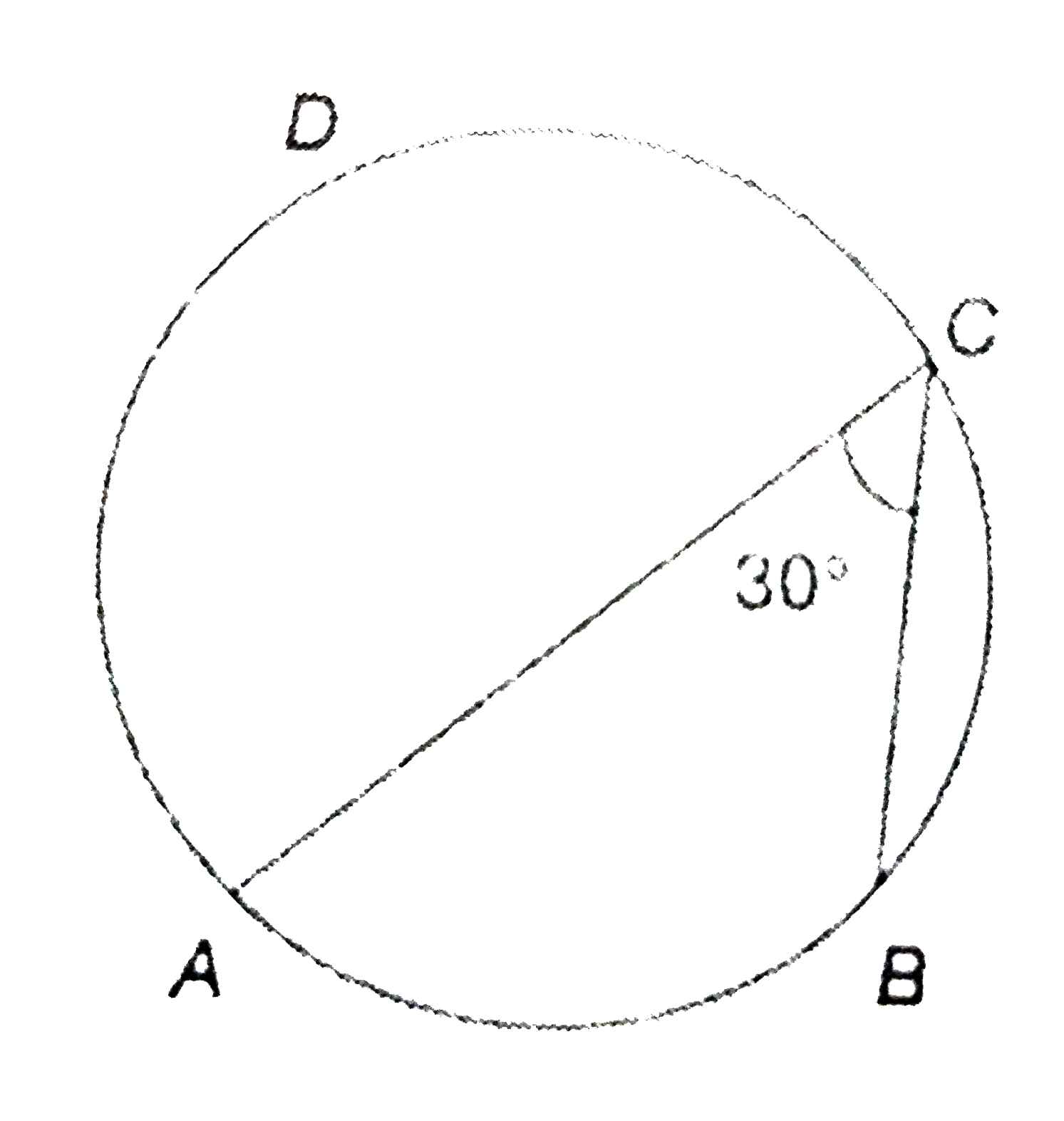
If AOB is a diameter of the circle and AC=BC, then ∠CAB is equal to
A30∘B45∘C60∘D90∘In the given figure, AB is the diameter of the circle. Find the value of ∠ACD:
 A30∘B60∘C45∘D25∘
A30∘B60∘C45∘D25∘In the figure, CDE is a straight line and A, B, C and D are points on the circle. ∠BCD=44∘, find the value of x.
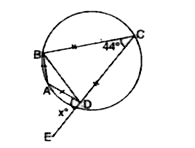 A44∘B68∘C90∘D56∘
A44∘B68∘C90∘D56∘
If AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionAB is a diameter of a circle and C is any point on the circle. Show that the area of ABC is maximum, when it is isosceles.
View SolutionIn the adjoining figure, AB is the diameter of the circle and two points C and D are on the circle. If ∠CAD=45∘ and ∠ABC=65∘, then find the value of ∠DCA.
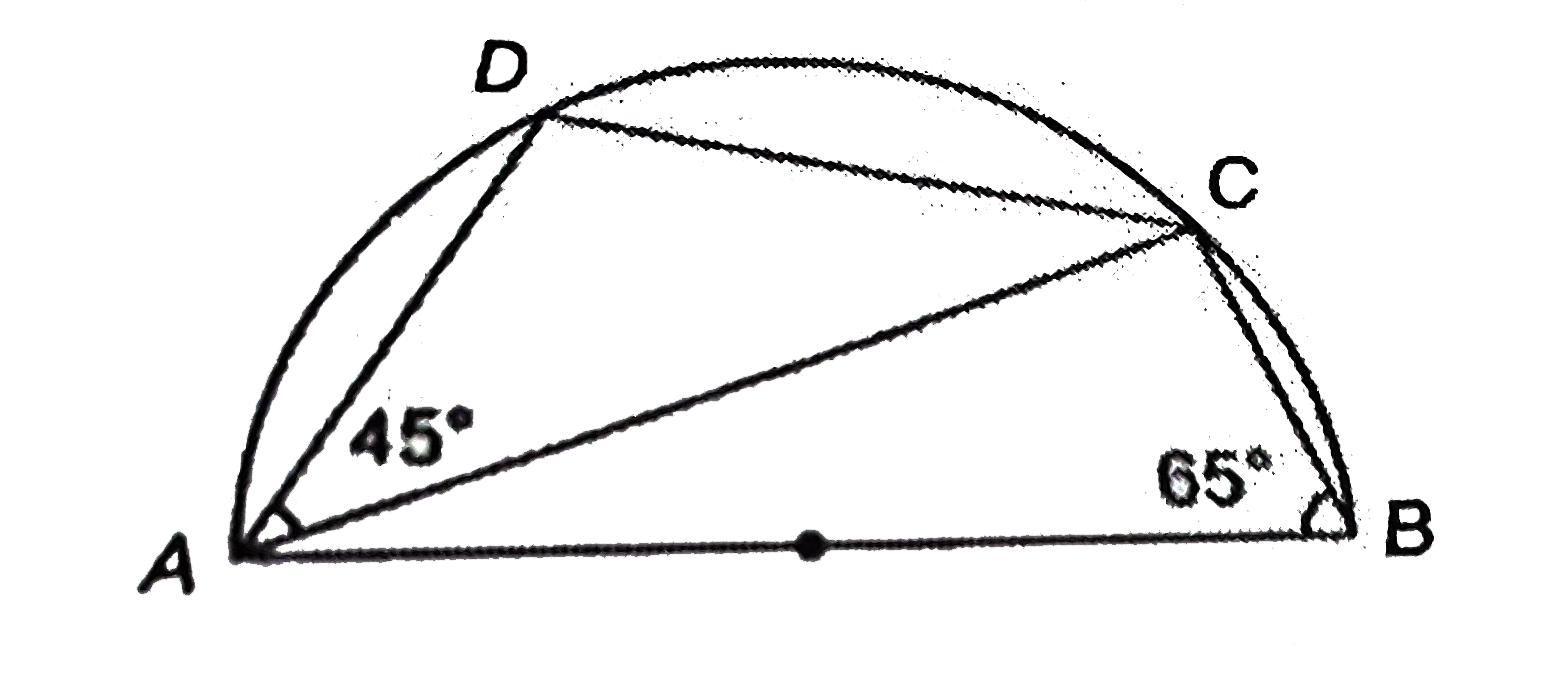
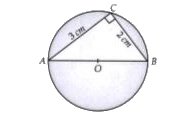
View SolutionIn the given figure, AOB is a diameter of a circle with centre O. Find tan A tan B.
View SolutionIf the given figure, AB is diameter of the circle, C and D lie on the semicircle. ∠ABC=65∘and∠CAD=45∘, find ∠DCA.
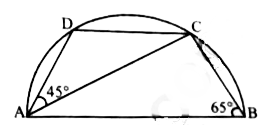
View Solution