Question

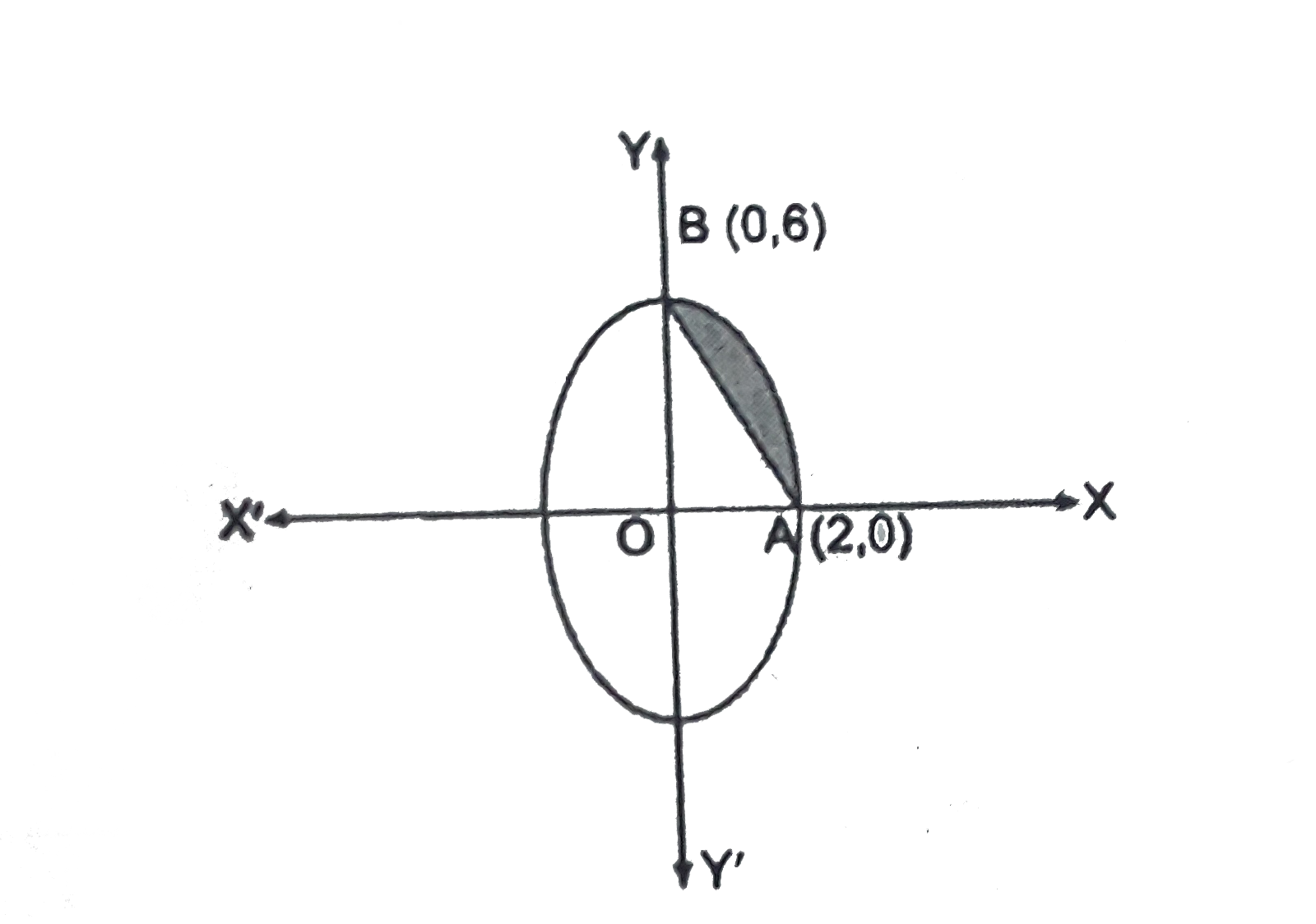
In Figure, AOBA is the part of the ellipse $9x^2+y^2=36$in the first quadrant such that $OA=2andOB=6$. Find the area between the arc AB and the chord AB.

Explanation

To solve the problem of finding the area between the arc AB and the chord AB for the ellipse given by the equation $$9x^2+y^2=36$$ in the first quadrant, we can follow these steps:

Step 1: Identify the ellipse parameters
The equation of the ellipse can be rewritten in standard form:
\( \frac{x^2}{4} + \frac{y^2}{36} = 1 \)
From this, we can identify \(a^2 = 4\) and \(b^2 = 36\), which gives us \(a = 2\) and \(b = 6\).

Step 2: Find the coordinates of points A and B
Given that \(OA = 2\) and \(OB = 6\), we can find the coordinates of points A and B:
- Point A is at \((2, 0)\) since it lies on the x-axis.
- Point B is at \((0, 6)\) since it lies on the y-axis.

Step 3: Find the equation of the chord AB
To find the equation of the line (chord) connecting points A and B, we can use the two-point form of the line equation:
\( y - y_1 = m(x - x_1) \)
where \(m\) is the slope given by:
\( m = \frac{y_2 - y_1}{x_2 - x_1} = \frac{6 - 0}{0 - 2} = -3 \)
Using point A \((2, 0)\):
\( y - 0 = -3(x - 2) \implies y = -3x + 6 \)

Step 4: Set up the area calculation
The area between the arc AB and the chord AB can be computed using integration. We will find the area under the ellipse from \(x = 0\) to \(x = 2\) and subtract the area under the line from \(x = 0\) to \(x = 2\).

Step 5: Find the area under the ellipse
To find the area under the ellipse, we first express \(y\) in terms of \(x\):
\( y = \sqrt{36 - 9x^2} = 6\sqrt{1 - \frac{x^2}{4}} \)
The area under the ellipse from \(x = 0\) to \(x = 2\) is given by:
\( \text{Area}_{\text{ellipse}} = \int_0^2 6\sqrt{1 - \frac{x^2}{4}} \, dx \)

Step 6: Find the area under the chord
The area under the line \(y = -3x + 6\) from \(x = 0\) to \(x = 2\) is:
\( \text{Area}_{\text{line}} = \int_0^2 (-3x + 6) \, dx \)

Step 7: Calculate the integrals
1. For the ellipse:
\( \text{Area}_{\text{ellipse}} = \int_0^2 6\sqrt{1 - \frac{x^2}{4}} \, dx \)
Using the substitution \(x = 2\sin(\theta)\), \(dx = 2\cos(\theta)d\theta\):
\( = 12 \int_0^{\frac{\pi}{2}} \cos^2(\theta) \, d\theta = 12 \cdot \frac{\pi}{4} = 3\pi \)

2. For the line:
\( \text{Area}_{\text{line}} = \int_0^2 (-3x + 6) \, dx = \left(-\frac{3x^2}{2} + 6x\right)_0^2 = \left(-\frac{3(4)}{2} + 12\right) = 6 \)

Step 8: Find the area between the arc and the chord
The area between the arc AB and the chord AB is:
\( \text{Area}_{\text{between}} = \text{Area}_{\text{ellipse}} - \text{Area}_{\text{line}} = 3\pi - 6 \)

Final Answer
The area between the arc AB and the chord AB is:
\( \boxed{3\pi - 6} \)