In figure, find the area of the shaded region [Useπ=3.14]
To find the area of the shaded region in the given figure, we will break down the problem into manageable steps.
1. Identify the Areas:
- Let’s denote the areas involved:
- Area 1 (A1): The area of the larger semicircle.
- Area 2 (A2): The area of the first smaller semicircle.
- Area 3 (A3): The area of the second smaller semicircle.
- Note that A2 = A3 since both are semicircles with the same diameter.
2. Calculate Area 1 (A1):
- The radius of the larger semicircle is given as 14 cm.
- The formula for the area of a semicircle is:
A=12πr2
- Substituting the radius:
A1=12×3.14×(14)2
- Calculate 142:
142=196
- Now substitute back:
A1=12×3.14×196=98×3.14=307.72 cm2
3. Calculate Area 2 (A2):
- The diameter of the smaller semicircles is given as 14 cm, so the radius (r2) is:
r2=142=7 cm
- Using the semicircle area formula:
A2=12π(7)2
- Calculate 72:
72=49
- Substitute back:
A2=12×3.14×49=24.5×3.14=77.63 cm2
4. Calculate Area 3 (A3):
- Since A2 = A3, we have:
A3=A2=77.63 cm2
5. Total Area of the Shaded Region:
- The total area of the shaded region is:
A=A1+A2+A3
- Substitute the values:
A=307.72+77.63+77.63
- Calculate:
A=307.72+155.26=462.98 cm2
Final Answer:
The area of the shaded region is approximately 462.98 cm².
- Let’s denote the areas involved:
- Area 1 (A1): The area of the larger semicircle.
- Area 2 (A2): The area of the first smaller semicircle.
- Area 3 (A3): The area of the second smaller semicircle.
- Note that A2 = A3 since both are semicircles with the same diameter.
- The radius of the larger semicircle is given as 14 cm.
- The formula for the area of a semicircle is:
A=12πr2
- Substituting the radius:
A1=12×3.14×(14)2
- Calculate 142:
142=196
- Now substitute back:
A1=12×3.14×196=98×3.14=307.72 cm2
- The diameter of the smaller semicircles is given as 14 cm, so the radius (r2) is:
r2=142=7 cm
- Using the semicircle area formula:
A2=12π(7)2
- Calculate 72:
72=49
- Substitute back:
A2=12×3.14×49=24.5×3.14=77.63 cm2
- Since A2 = A3, we have:
A3=A2=77.63 cm2
- The total area of the shaded region is:
A=A1+A2+A3
- Substitute the values:
A=307.72+77.63+77.63
- Calculate:
A=307.72+155.26=462.98 cm2
The area of the shaded region is approximately 462.98 cm².
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the joining figure , find the area of the shaded region.
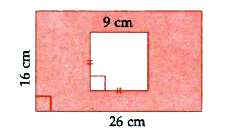 A325cm2B245cm2C335cm2D185cm2
A325cm2B245cm2C335cm2D185cm2
Find the area of the shaded region in figure.

View SolutionFind the area of the shaded region in Figure.
View SolutionIn Figure, OABC is a squaer inscribed in a quadrant OPBQ. If OA=20cm, find the are of shaded region. [Useπ=3.14.]
View SolutionIn the given figure, PQ = 24 cm PR = 7 cm and O is the centre of the circle. Find the area of the shaded region. (Use π=3.14)

View SolutionIn the given figure square OABC is inscribed in a sector OPBQ. If OC = 20 cm, find the area of the shaded region (Use π=3.14)

View SolutionIn Fig. an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π=3.14 )
View SolutionIn Figure , ABCD is a prallelogram. A semicircle with centre O and the diameter AB has been drawn and it passes through D. If AB = 12 cm and OD ⊥ AB. Then find the area of the shaded region. (Use π=3.14)
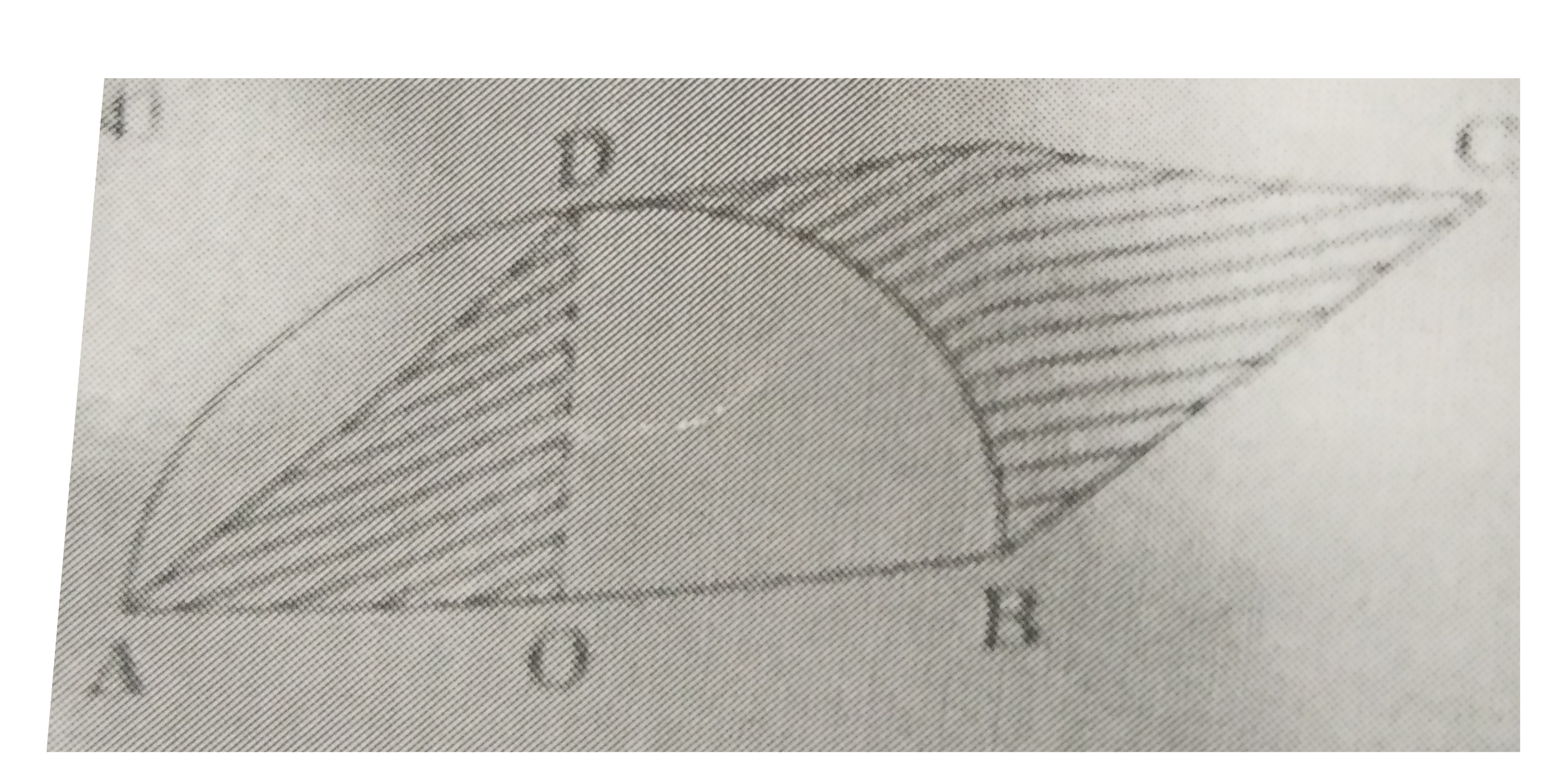
View Solution
