In Fig. 12.31, a square OABC is inscribed in a quadrant OPBQ. If OA=20cm,find the area of the shaded region. (Useπ=3.14)
To solve the problem of finding the area of the shaded region in the figure with a square OABC inscribed in a quadrant OPBQ, we can follow these steps:
Step 1: Find the area of the square OABC.
Given that the side of the square OA = 20 cm, we can calculate the area of the square using the formula:
Area of square=side2=OA2=202=400 cm2
Step 2: Determine the radius of the quadrant OPBQ.
The radius of the quadrant OPBQ can be found using the Pythagorean theorem. Since OABC is a square, the lengths OA and AB are equal, and we can denote them as:
- OA = 20 cm
- AB = 20 cm
According to the Pythagorean theorem:
OB2=OA2+AB2
Substituting the values:
OB2=202+202=400+400=800
Taking the square root to find OB:
OB=√800=20√2 cm
Step 3: Calculate the area of the quadrant OPBQ.
The area of a quadrant is one-fourth of the area of a circle. The area of a circle is given by πr2. Therefore, the area of the quadrant is:
Area of quadrant=14×π×(OB)2
Substituting OB=20√2 and π=3.14:
Area of quadrant=14×3.14×(20√2)2
Calculating (20√2)2:
(20√2)2=400×2=800
Now substituting back:
Area of quadrant=14×3.14×800=3.14×200=628 cm2
Step 4: Find the area of the shaded region.
The area of the shaded region is the area of the quadrant minus the area of the square:
Area of shaded region=Area of quadrant−Area of square
Substituting the values we calculated:
Area of shaded region=628 cm2−400 cm2=228 cm2
Final Answer:
The area of the shaded region is 228 cm².
---
Given that the side of the square OA = 20 cm, we can calculate the area of the square using the formula:
The radius of the quadrant OPBQ can be found using the Pythagorean theorem. Since OABC is a square, the lengths OA and AB are equal, and we can denote them as:
- AB = 20 cm
The area of a quadrant is one-fourth of the area of a circle. The area of a circle is given by πr2. Therefore, the area of the quadrant is:
The area of the shaded region is the area of the quadrant minus the area of the square:
The area of the shaded region is 228 cm².
Topper's Solved these Questions
- AREAS RELATED TO CIRCLESBOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - Exercise 12.2
14 Videos
- AREAS RELATED TO CIRCLESBOOK - NCERT ENGLISHCHAPTER - AREAS RELATED TO CIRCLESEXERCISE - EXERCISE 12.1
5 Videos
- ARITHMETIC PROGRESSIONSBOOK - NCERT ENGLISHCHAPTER - ARITHMETIC PROGRESSIONSEXERCISE - All Questions
65 Videos
Similar Questions
In Figure, OABC is a squaer inscribed in a quadrant OPBQ. If OA=20cm, find the are of shaded region. [Useπ=3.14.]
View SolutionIn figure, find the area of the shaded region [Useπ=3.14]
View SolutionIn figure, find the area of the shaded region [Useπ=3.14]
View SolutionIn Fig. 15.99, a square OABC is inscribed in a quadrant OPBQ of a circle. If OA=21 cm , find the area of the shaded region. (FIGURE)
View SolutionIn the given figure square OABC is inscribed in a sector OPBQ. If OC = 20 cm, find the area of the shaded region (Use π=3.14)

View SolutionIn the given figure, find the area of the shaded region [Useπ=3.14]
View SolutionIn Figure, PQRS is a square of side 4 cm. Find the area of the shaded region.
View SolutionIn Fig. an equilateral triangle ABC of side 6 cm has been inscribed in a circle. Find the area of the shaded region. (Take π=3.14 )
View SolutionIn Figure , a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, find the area of the shaded region
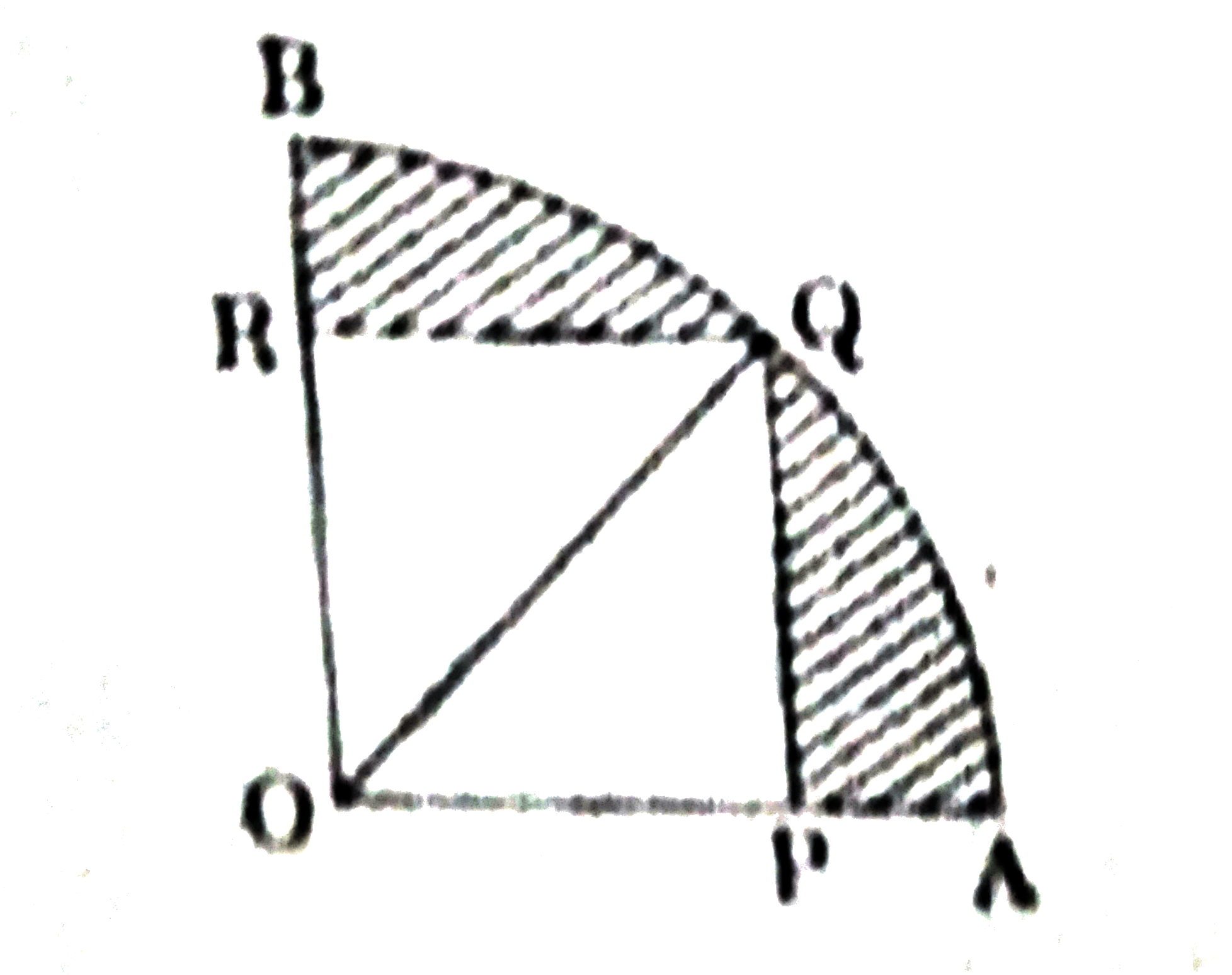
View SolutionIn Figure-9, a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, Find the area of the shaded region.
View Solution
