In figure, if AOB is a diameter and ∠ADC=120∘,then∠CAB=30∘.
Video Solution
Text Solution
The correct Answer is:1
Join CA and CB.
Since, ADCB is a cyclic quadrilateral.
∴∠ADC+∠CBA=180∘.
[sum of opposite angles of cyclic quadrilateral is 180∘]
⇒∠CBA=180∘−120∘=60∘[∵∠ADC=120∘]
InΔACB,∠CAB+∠CBA+∠ACB=180∘
[by angle sum property of a triangle]
∴∠CAB+60∘+90∘=180∘
[triangle formed from diameter to the circle is 90∘i.e.,∠ACB=90∘]
⇒∠CAB=180∘−150∘=30∘
|
Topper's Solved these Questions
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Exercise 10.4
2 Videos
- Areas of Parallelograms and TrianglesBOOK - NCERT EXEMPLARCHAPTER - Areas of Parallelograms and TrianglesEXERCISE - Areas Of Parallelograms And Triangles
34 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Long Answer Type Questions
5 Videos
Similar Questions
Knowledge Check
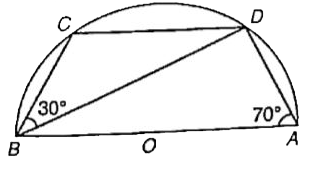
In the given figure, AB is the diameter. ∠BAD=70∘and∠DBC=30∘. Find ∠BDC :
 A25∘B30∘C40∘D60∘
A25∘B30∘C40∘D60∘In figure, BC is a diameter of the circle and ∠BAO=60∘. Then,∠ADCis equal to
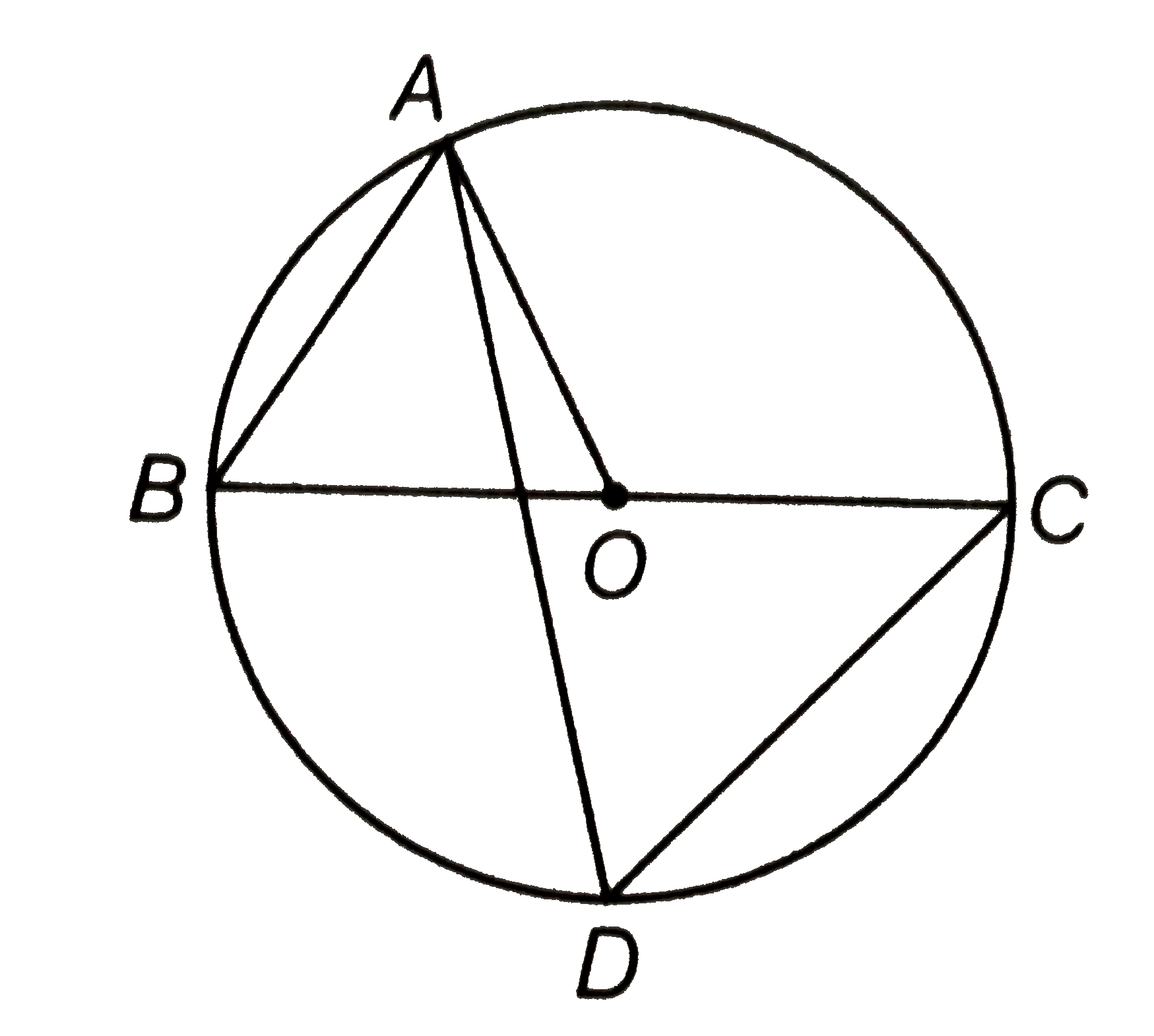 A60∘B45∘C50∘D120∘
A60∘B45∘C50∘D120∘In the given figure, AB is the diameter of the circle, ∠ADC=120∘. Find ∠CAB:
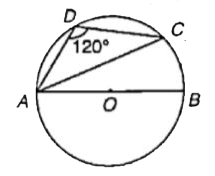 A20∘B30∘C40∘Dcan't be determined
A20∘B30∘C40∘Dcan't be determined
In the following figure, O is the centre of the circle , AC is the diameter and if ∠APB=120∘ , then find ∠BQC .
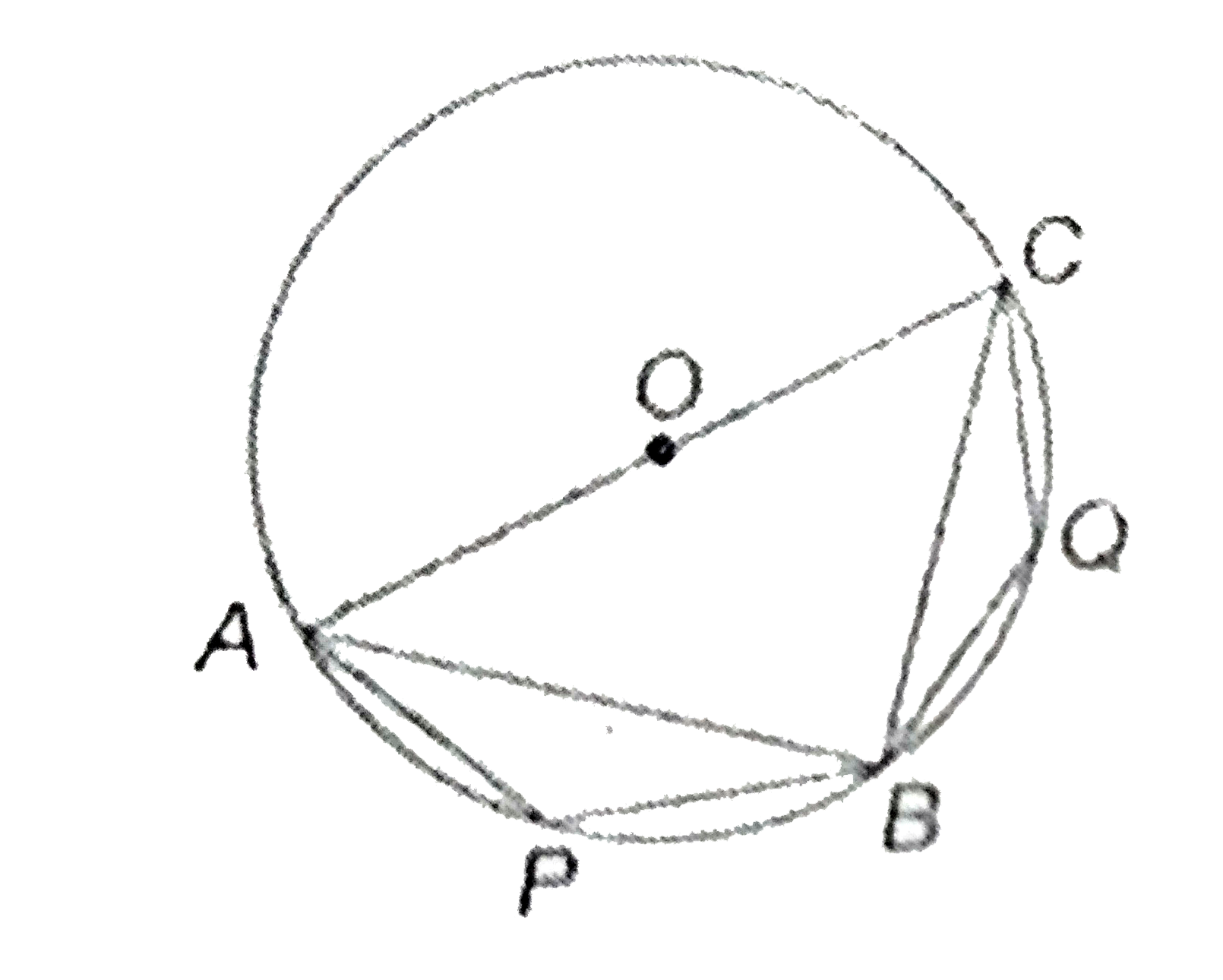
View SolutionIn the given figure, AB is the diameter of the circle. ∠ADC=120∘. Find ∠CAB :

View SolutionIn the given figure O is the centre of circle and ∠BOC=30∘,∠AOB=60∘ If there is a point D on the circle, not on arc ABC, then find ∠ADC

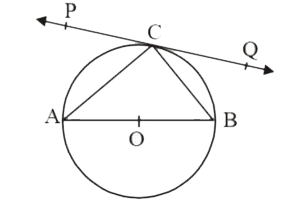
View SolutionIn figure PQ is a tangent at a point C to a circle with centre O. If AB is a diameter and ∠CAB=30∘, find ∠PCA
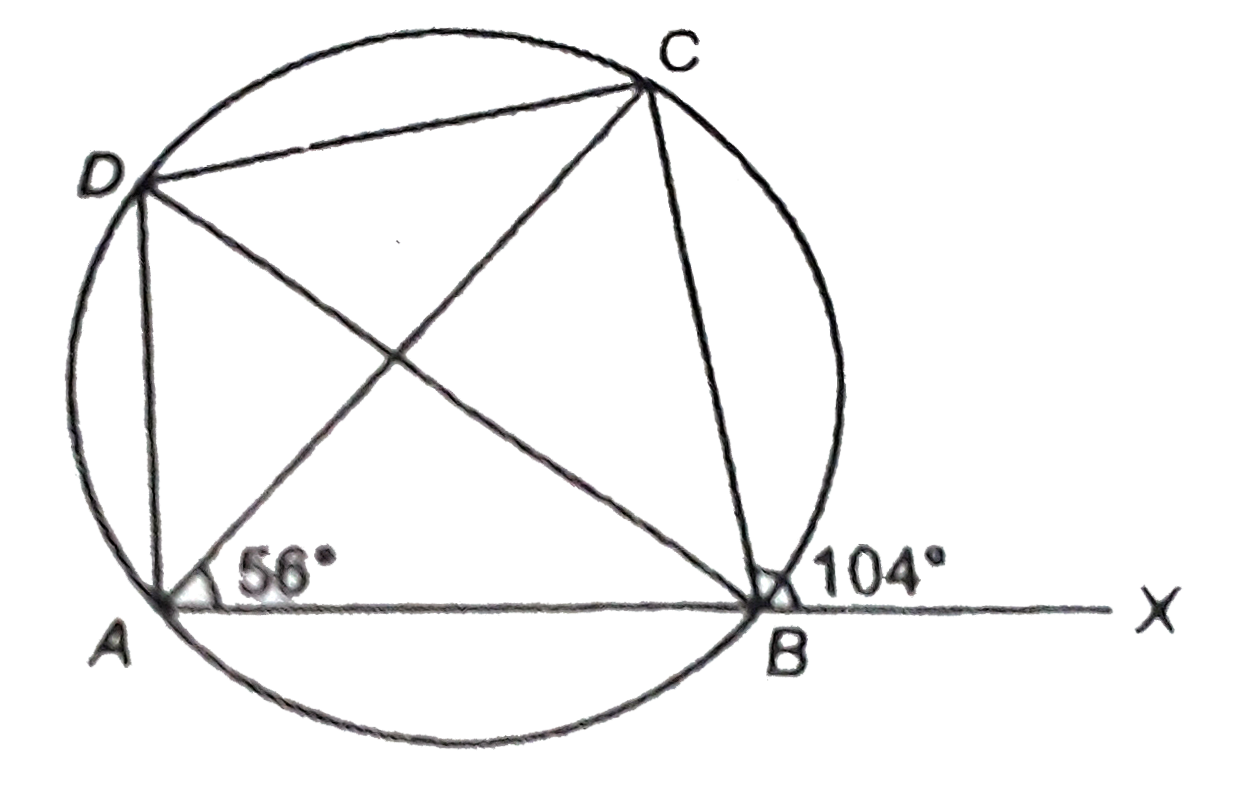
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral . If ∠CBX=104∘ and ∠CAB=56∘, then find the value of ∠ADB.
View Solution