In figure O is the centre of the circle, prove that ∠z=∠x+∠y.

∠1=∠2 (angles in the same segment of a circle are equal
∠z=2∠1 (subtended by an arc AB)
∴∠z=∠1+∠2 (∵∠1=∠2)
⇒∠z=∠y−∠3+∠2 (∵exterior of∠y=∠1+∠3)
=∠y−∠3+∠x+∠3 (∵exteriorof∠2=∠x+∠3)
Hence, ∠z=∠x+∠y.
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
In the adjoining figure, O is the centre of the circle, Prove that ∠x=∠y+∠z.

View SolutionIn the adjoining figure, P is the centre of the circle. Prove that ∠XPZ=2(∠XZY+∠YXZ).
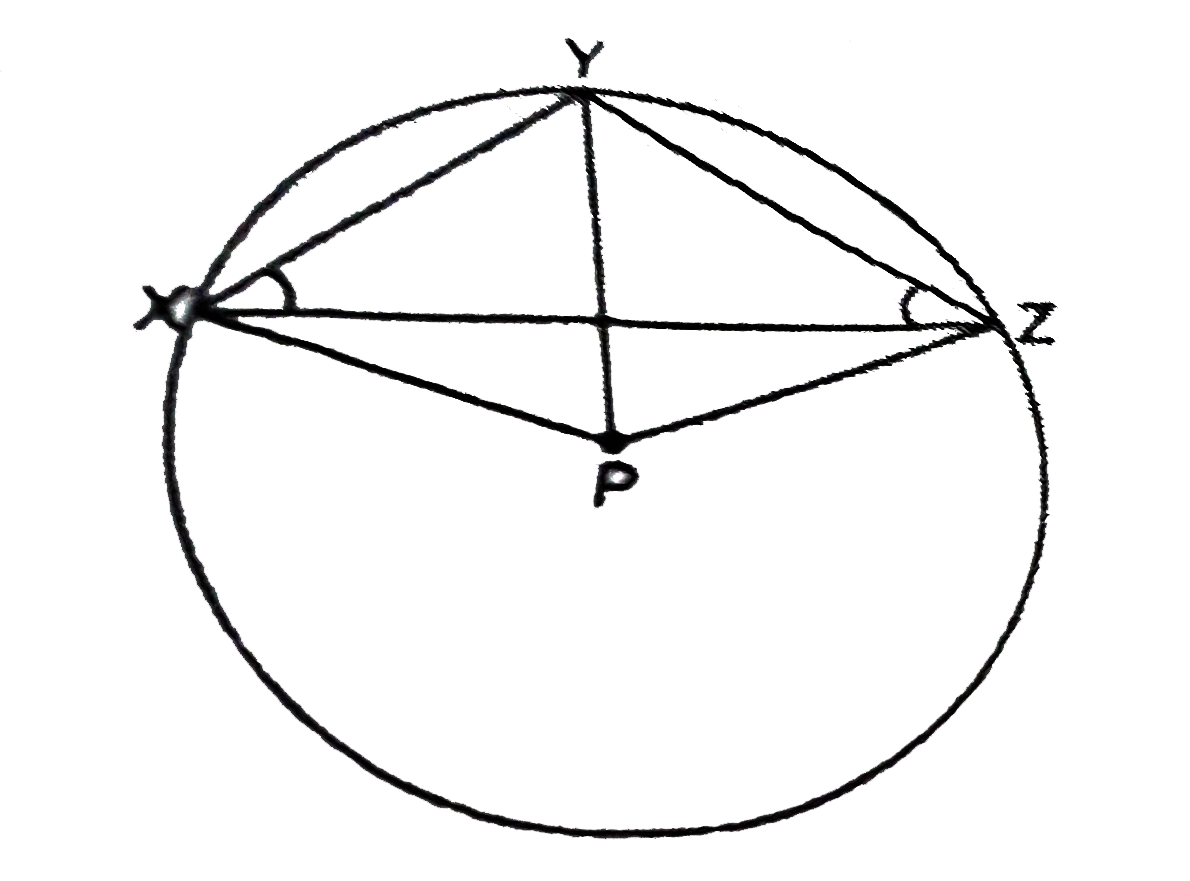
View SolutionIn Figure, O is the centre of the circle, prove that ∠x=∠y+∠z
View SolutionIn Figure, O is the centre of the circle. Find ∠BAC
View SolutionIn Figure, O is the centre of the circle. Find ∠CBD
View SolutionIn the adjoining figure, O is the centre of the circle. Find the value of ∠BEC.
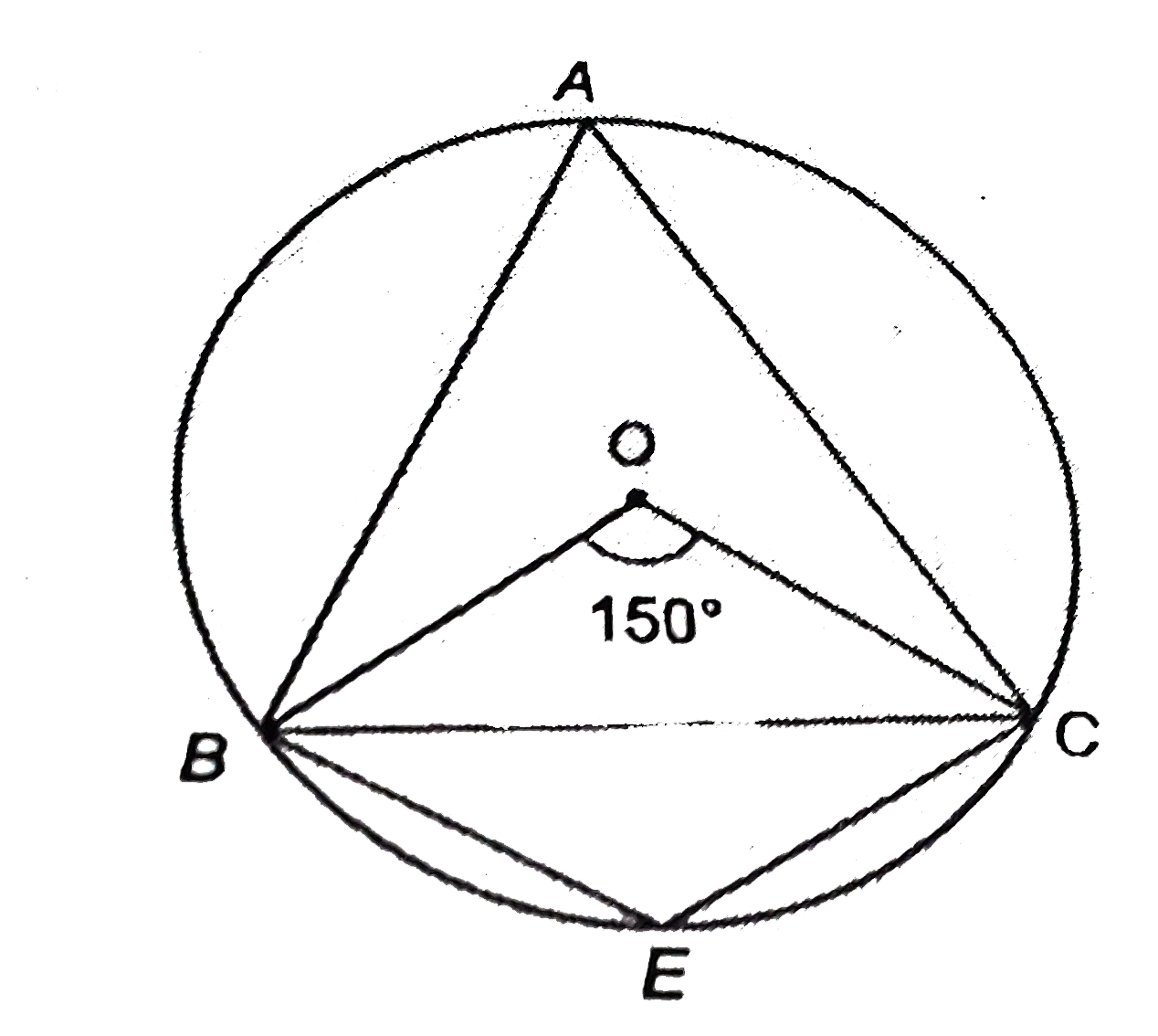
View SolutionIn the adjoining figure , O is the centre of the circle and ∠OAB=60∘. Find ∠APC.

View SolutionIn the adjoining figure, O is the centre of the circle. If ∠PAO=15∘ and ∠PBO=30∘, then find the value of ∠AOB.

View SolutionIn the figure O is the centre of the circle ∠AOE=150∘,∠DAO=51∘. Calculate the sizes of the angles CEB and OCE.
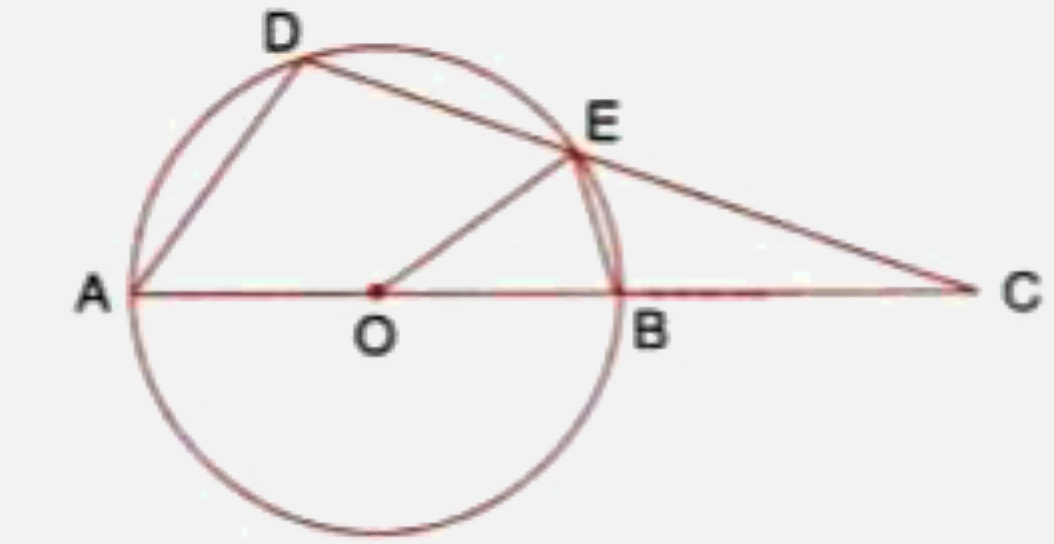
View SolutionIn the adjoining figure, O is the centre of the circle. If ∠AOB=150∘ and ∠BOC=100∘, then find the value of ∠ABC.

View Solution
