In figure, ⌢AB≅⌢AC and O is the centre of the circle,Prove that OA is the perpendicualr bisector of BC.
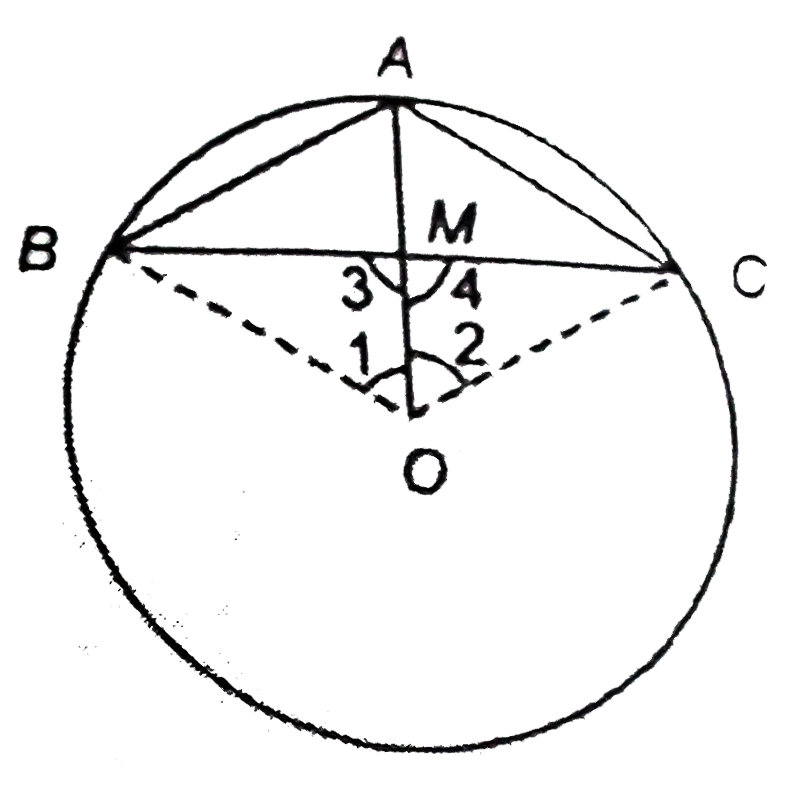
In figure, oversetfrown(AB)congoversetfrown(AC) and O is the centre of the circle,Prove that OA is the perpendicualr bisector of BC.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

Since ⌢AB≅⌢AC (given)
⇒AB=AC (corresponding chords of congruent arcs are equal)
In ΔOAB and ΔOAC,
∵ ⎧⎪⎨⎪⎩AB=AC(just proved)OA=OA(common)OB=OC(each radii)
∴ΔOAB≅ΔOAC (by SSS congruency)
∴∠1=∠2 (c.p.c.t)
Now, in ΔOMB and ΔOMC,
∵ ⎧⎪⎨⎪⎩OB=AC(each radii)∠1=∠2(just proved)OM=OM(common)
∴ΔOMB≅ΔOMC (by S.A.S. congruency)
∴BM=MC (c.p.c.t) .......(1)
Also, ∠3=∠4 (c.p.c.t)
But ∠3+∠4=180∘ (L.P.A.)
⇒∠3=∠4=90∘ ......(2)
From (1) and (2) , we get
OM is the perpendicular bisector of BC.
⇒OA is the perpendicular bisector of BC.

|
Class 9MATHSCIRCLES

Topper's Solved these Questions

Similar Questions