In Figure, PQRS is a cyclic quadrilateral. Find the measure of each of its angles.
To find the measures of the angles in the cyclic quadrilateral PQRS, we will use the property that the opposite angles of a cyclic quadrilateral are supplementary, meaning they add up to 180 degrees.
1. Identify the angles:
Let:
- Angle SPQ = 4y
- Angle SRQ = 6y
- Angle PSR = 7x
- Angle PQR = 5x
2. Set up the first equation using the property of cyclic quadrilaterals:
Since angle SPQ and angle SRQ are opposite angles, we can write:
Angle SPQ+Angle SRQ=180∘
Substituting the expressions for the angles:
4y+6y=180∘
Simplifying this gives:
10y=180∘
3. Solve for y:
Dividing both sides by 10:
y=180∘10=18∘
4. Set up the second equation:
Now, using the other pair of opposite angles (PSR and PQR):
Angle PSR+Angle PQR=180∘
Substituting the expressions for these angles:
7x+5x=180∘
Simplifying this gives:
12x=180∘
5. Solve for x:
Dividing both sides by 12:
x=180∘12=15∘
6. Calculate each angle:
- Angle SRQ = 6y=6×18∘=108∘
- Angle SPQ = 4y=4×18∘=72∘
- Angle PSR = 7x=7×15∘=105∘
- Angle PQR = 5x=5×15∘=75∘
Summary of the Angles:
- Angle SPQ = 72°
- Angle SRQ = 108°
- Angle PSR = 105°
- Angle PQR = 75°
Let:
- Angle SPQ = 4y
- Angle SRQ = 6y
- Angle PSR = 7x
- Angle PQR = 5x
Since angle SPQ and angle SRQ are opposite angles, we can write:
Angle SPQ+Angle SRQ=180∘
Substituting the expressions for the angles:
4y+6y=180∘
Simplifying this gives:
10y=180∘
Dividing both sides by 10:
y=180∘10=18∘
Now, using the other pair of opposite angles (PSR and PQR):
Angle PSR+Angle PQR=180∘
Substituting the expressions for these angles:
7x+5x=180∘
Simplifying this gives:
12x=180∘
Dividing both sides by 12:
x=180∘12=15∘
- Angle SRQ = 6y=6×18∘=108∘
- Angle SPQ = 4y=4×18∘=72∘
- Angle PSR = 7x=7×15∘=105∘
- Angle PQR = 5x=5×15∘=75∘
- Angle SPQ = 72°
- Angle SRQ = 108°
- Angle PSR = 105°
- Angle PQR = 75°
Topper's Solved these Questions
Similar Questions
In Figure, ABCD is a cyclic quadrilateral. Find the value of a and b.
View SolutionIn Figure, ABCD is a cyclic quadrilateral; O is the centre of the circle. If ∠BOD=1600, find the measure of ∠BPD
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral and AB is the diameter of the circle. If ∠APC=120∘, then find the value of ∠CAB.
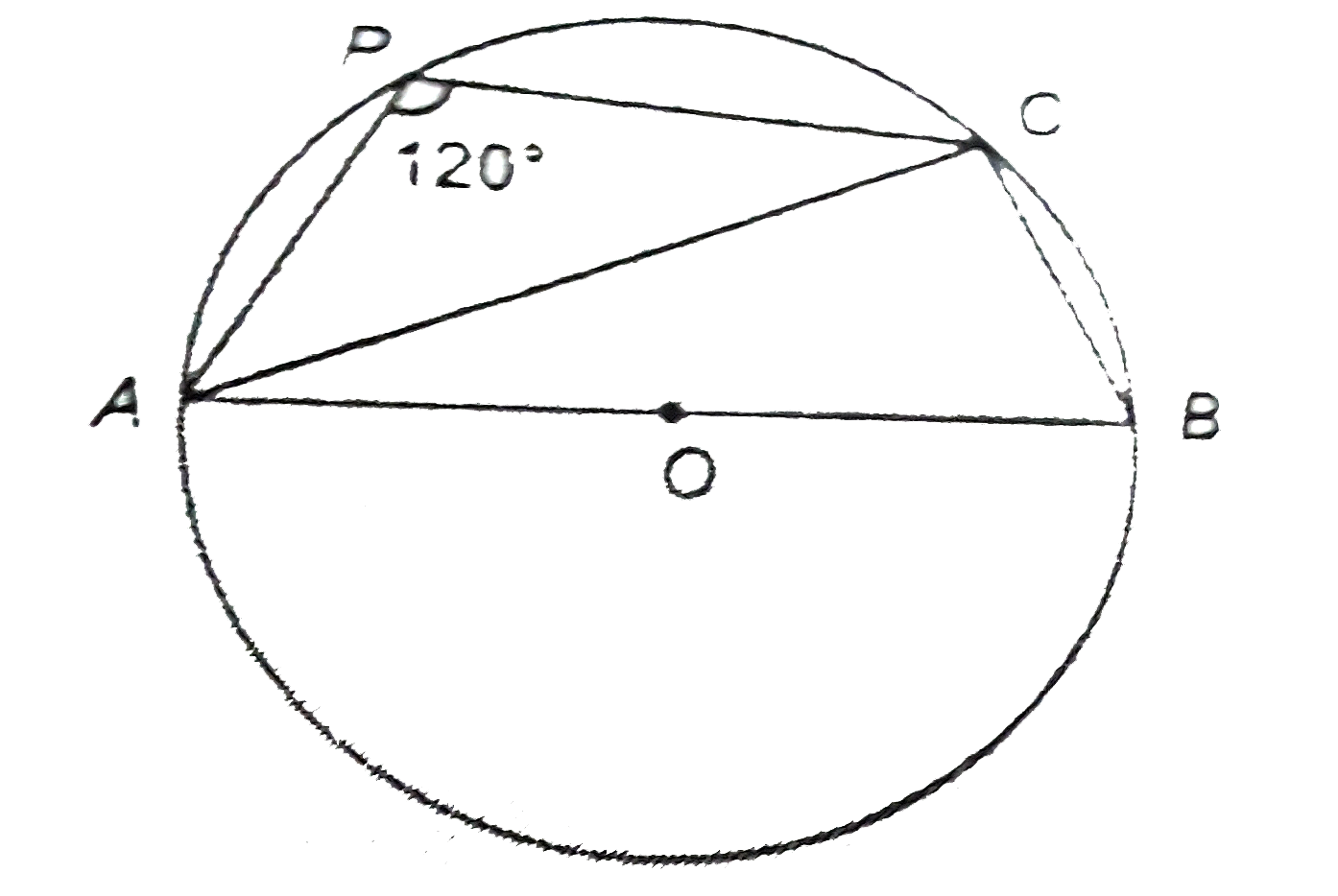
View SolutionIn the adjoining figure, if ABCD is a cyclic quadrilateral, find the value of x.
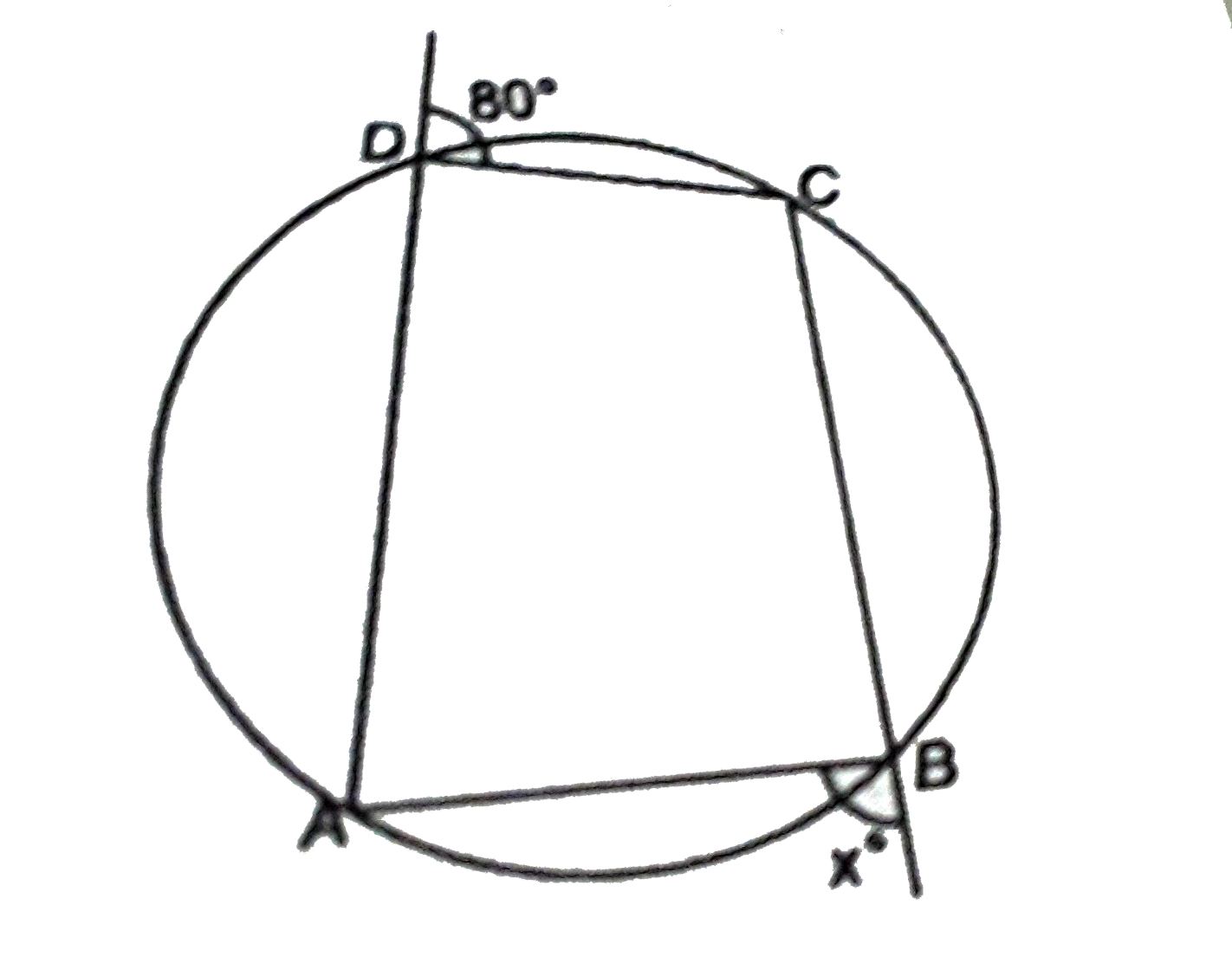
View SolutionIn the adjoining figure, ABCD is a cyclic quadrilateral whose side AB is the diameter of the circle . If ∠ADC=140∘ , then find the value of ∠BAC.
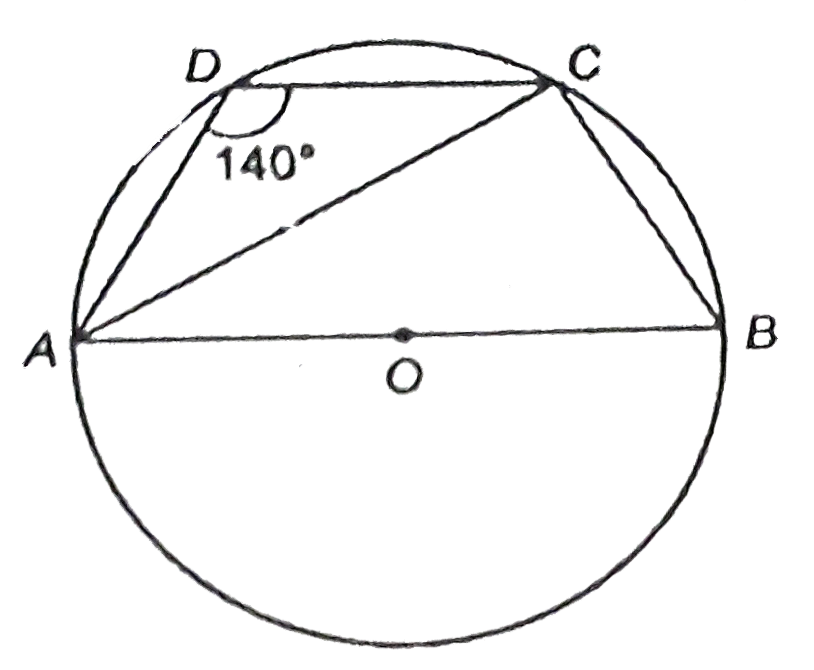
View SolutionIn cyclic quadrilateral ABCD,∠A=3∠C and ∠D=5∠B. Find the measure of each angle of the quadrilateral.
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q.
View SolutionIn Figure, PQRS is a quadrilateral in which diagonals PR and QS intersect in O . Show that PQ+QR+RS+SP>PR+QS PQ+QR+RS+SP<2 (PR+QS) Figure
View SolutionIn Figure, PQRS is a quadrilateral and T and U are respectively points on PS and RS such that PQ=RQ, ∠PQT=∠RQU and ∠TQS=∠UQS. Prove that QT=QU.
View SolutionIf PQRS is a square, then write the measure of ∠SRP
View Solution
