In cyclic quadrilateral ABCD,∠A=3∠C and ∠D=5∠B. Find the measure of each angle of the quadrilateral.
The correct Answer is:∠A=135∘,∠B=30∘,∠C=∠45∘;∠D=150∘
To find the measures of each angle of the cyclic quadrilateral ABCD, where ∠A = 3∠C and ∠D = 5∠B, we can follow these steps:
Step 1: Set up the equations based on the properties of cyclic quadrilaterals.
In a cyclic quadrilateral, the sum of opposite angles is 180 degrees. Therefore, we can write:
1. ∠A + ∠C = 180° (1)
2. ∠B + ∠D = 180° (2)
Step 2: Substitute the relationships into the equations.
From the problem, we know:
- ∠A = 3∠C (3)
- ∠D = 5∠B (4)
Step 3: Substitute equation (3) into equation (1).
Using equation (3) in equation (1):
3∠C + ∠C = 180°
4∠C = 180°
∠C = 180° / 4
∠C = 45°
Step 4: Find ∠A using the value of ∠C.
Now that we have ∠C, we can find ∠A:
∠A = 3∠C = 3 × 45° = 135°
Step 5: Substitute equation (4) into equation (2).
Now, we will use equation (4) in equation (2):
∠B + 5∠B = 180°
6∠B = 180°
∠B = 180° / 6
∠B = 30°
Step 6: Find ∠D using the value of ∠B.
Now that we have ∠B, we can find ∠D:
∠D = 5∠B = 5 × 30° = 150°
Step 7: Summarize the results.
Now we have all the angles of the cyclic quadrilateral:
- ∠A = 135°
- ∠B = 30°
- ∠C = 45°
- ∠D = 150°
Final Answer:
The measures of the angles in the cyclic quadrilateral ABCD are:
- ∠A = 135°
- ∠B = 30°
- ∠C = 45°
- ∠D = 150°
---
In a cyclic quadrilateral, the sum of opposite angles is 180 degrees. Therefore, we can write:
1. ∠A + ∠C = 180° (1)
2. ∠B + ∠D = 180° (2)
From the problem, we know:
- ∠A = 3∠C (3)
- ∠D = 5∠B (4)
Using equation (3) in equation (1):
3∠C + ∠C = 180°
4∠C = 180°
∠C = 180° / 4
∠C = 45°
Now that we have ∠C, we can find ∠A:
∠A = 3∠C = 3 × 45° = 135°
Now, we will use equation (4) in equation (2):
∠B + 5∠B = 180°
6∠B = 180°
∠B = 180° / 6
∠B = 30°
Now that we have ∠B, we can find ∠D:
∠D = 5∠B = 5 × 30° = 150°
Now we have all the angles of the cyclic quadrilateral:
- ∠A = 135°
- ∠B = 30°
- ∠C = 45°
- ∠D = 150°
The measures of the angles in the cyclic quadrilateral ABCD are:
- ∠A = 135°
- ∠B = 30°
- ∠C = 45°
- ∠D = 150°
Topper's Solved these Questions
- TANGENTS AND INTERSECTING CHORDSBOOK - ICSECHAPTER - TANGENTS AND INTERSECTING CHORDSEXERCISE - EXERCISE 18 (B)
18 Videos
- SPECIMEN QUESTION PAPER (MATHEMATICS)BOOK - ICSECHAPTER - SPECIMEN QUESTION PAPER (MATHEMATICS)EXERCISE - Section C
12 Videos
- TRIGONOMETRICAL IDENTITIESBOOK - ICSECHAPTER - TRIGONOMETRICAL IDENTITIESEXERCISE - QUESTIONS
22 Videos
Similar Questions
In a cyclic quadrilateral ABCD , if ∠A=3∠C. Find ∠A
View SolutionIn a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1:2:4:5. Find the measure of each angle of the quadrilateral.
View SolutionIn a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1:2:4:5 . Find the measure of each angles of the quadrilateral.
View SolutionIn a quadrilateral ABCD, the angles A, B, C and D are in the ratio 1:2:3:4 . Find the measure of each angle of the quadrilateral.
View SolutionIn a quadrilateral ABCD , the angles A, B, C and D are in the ratio 1:2:3:4. Find the measure of each angles of the quadrilateral.
View Solution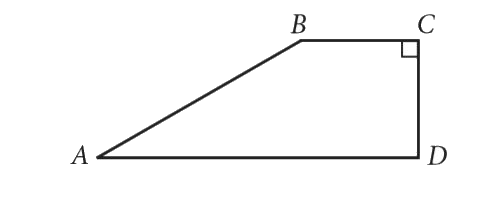
In quadrilateral ABCD above , ¯¯¯¯¯¯AD¯¯¯¯¯¯BC and CD=12AB. What is the measure of angle B ?
View SolutionIn a cyclic quadrilateral ABCD, if AB || CD and ∠B=700, find the remaining angles.
View SolutionIn Figure, PQRS is a cyclic quadrilateral. Find the measure of each of its angles.
View SolutionIn Figure, PQRS is a cyclic quadrilateral. Find the measure of each of its angles.
View SolutionIn a cyclic quadrilateral ABCD ∠A:∠C=3:1and angle B : angle D = 1 : 5 find each angle of the quadrilateral
View Solution