In Figure, PQ∣∣RS, ∠AEF=950, ∠BHS=1100 and ∠ABC=x0. Then the value of x is (a)150 (b) 250 (c) 700 (d) 350
Solution
'PQ || RS'
Also, '/_AEF' and '/_1' are the corresponding angles.If a transversal intersects two parallel lines, then each pair of corresponding angles are equal.Therefore,
'/_1 = /_AEF'
It is given that
'/_AEF = 95@'
Therefore,
'/_1 = 95@'
Clearly, '/_1' and '/_2' form a linear pair, therefore, their sum must be supplementary.
Therefore,
'/_1+/_2=180@'
On substituting '/_1 = 95@' in equation above, we get:
'95@+/_2=180@'
'/_2 = '180@ - 95@'
'/_2=/_85@'
In '/_\BHG':
We know that, in a triangle exterior angle is equal to the sum of the interior opposite angles. Therefore,
'/_2+x= /_BHS'
Substituting '/_BHS =110@'
and '/_2 = 85@', we get:'X = 110@ - 85@'
'x = 25@'
Topper's Solved these Questions
Similar Questions
In Fig.102, ABCDEF, ∠ABG=1100,∠GCD=1000 and ∠BGC=x0. the value of x is (a) 35 (b) 50 (c) 30 (d) 40
View SolutionIn Fig.84, ABCD and AECF; ∠FCG=900 and ∠BAC=1200. Find the values of x,y and z.
View SolutionIn Figure, if AB∣∣CD, ∠APQ=500AND ∠PRD=1270, find x and y
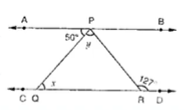
View SolutionIn Fig.92, AOB is a straight line such that ∠AOC=(3x+10)0, ∠COD=500 and ∠BOD=(x−8)0. The value of x is (a) 32 (b) 36 (c) 42 (d) 52
View SolutionIn Fig.103, PQRS and ∠PAB=600 and ∠ACS=1000. Then, ∠BAC= (a) (b)(c)(d)(e)40(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)60(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)80(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)50(q)0(r)(s)(t) (u)
View SolutionIn a parallelogram ABCD, if ∠A=(3x−20)∘,∠B=(y+15)∘,∠C=(x+40)∘, then find the values of xandy
View SolutionIn a rhombus ABCD, if ∠ACB=40∘, then ∠ADB=(a) 70∘ (b) 45∘ (c) 50∘ (d) 60∘
View SolutionIn Fig.104, ABCD, ∠OAB=1500 and ∠OCD=1200. Then, ∠AOC= (a) (b)(c)(d)(e)80(f)0(g)(h)(i) (j) (b) (k)(l)(m)(n)90(o)0(p)(q)(r) (s) (c) (d)(e)(f)(g)70(h)0(i)(j)(k) (l) (d) (m)(n)(o)(p)100(q)0(r)(s)(t) (u)
View SolutionIn ABC, ∠B=∠C and ray AX bisects the exterior angle ∠DAC.If ∠DAX=700, then ∠ACB= 350 (b) 900 (c) 700 (d) 550
View SolutionIf ABC and DEF are two triangles such that ABC ≅FDE and AB=5cm, ∠B=400 and ∠A=800. Then, which of the following is true? DF=5cm, ∠F=600 (b) DE=5cm, ∠E=600 DF=5 cm, ∠E=600 (d) DE=5cm, ∠D=400
View Solution
