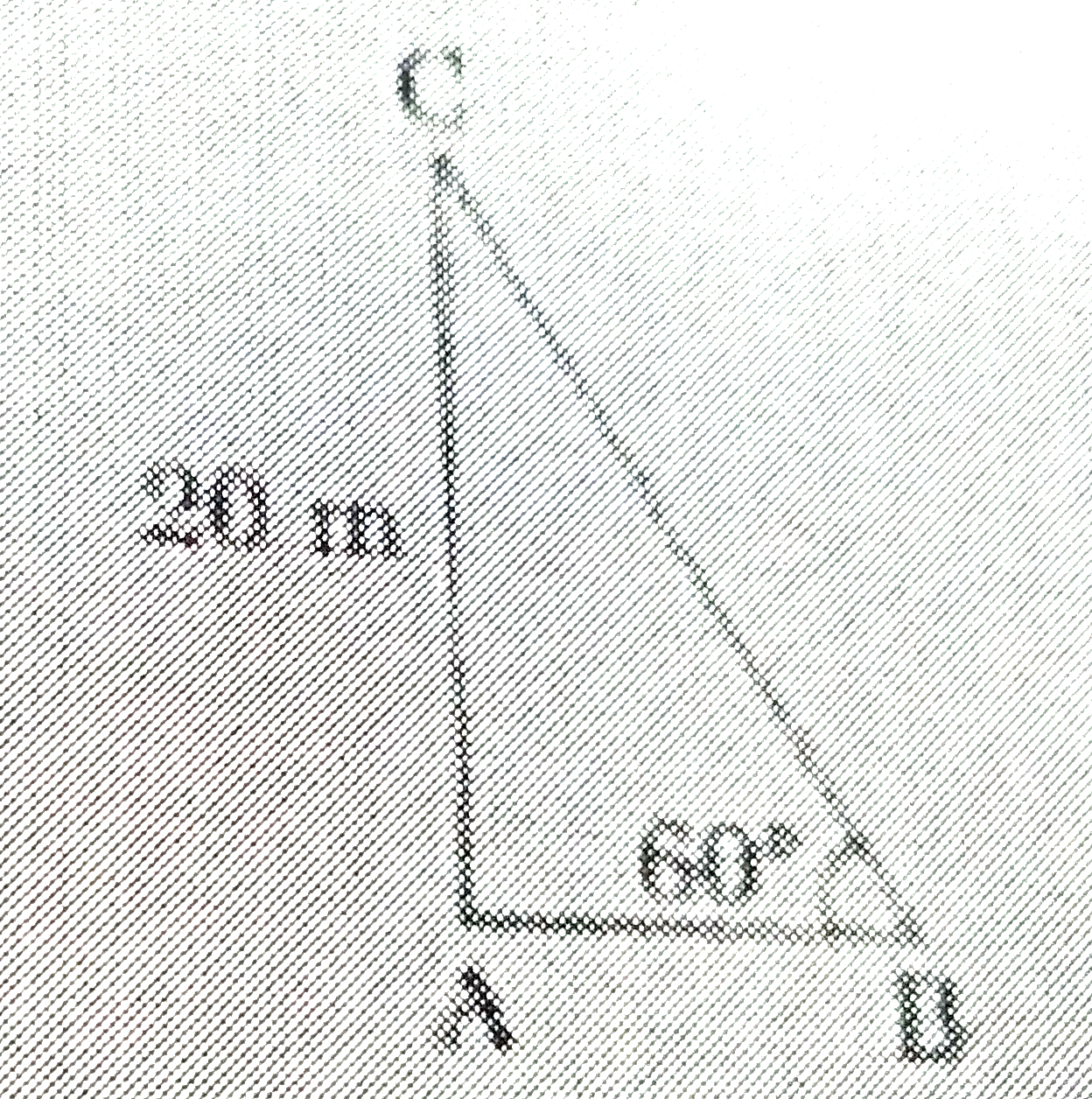
In figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
To solve the problem, we will use the properties of right triangles and trigonometric ratios.
1. Understand the Problem: We have a tower AC with a height of 20 meters. From a point B on the ground, the angle of elevation to the top of the tower (point A) is 60 degrees. We need to find the horizontal distance (BC) from point B to the foot of the tower (point C).
2. Draw the Diagram:
- Draw a vertical line representing the tower AC.
- Mark point C at the base of the tower.
- Mark point B on the ground such that angle ABC is 60 degrees.
- The height AC = 20 m.
3. Identify the Triangle:
- Triangle ABC is a right triangle where:
- AC (height of the tower) = 20 m
- Angle ABC = 60 degrees
- BC (distance from point B to the foot of the tower) is what we need to find.
4. Use the Tangent Function:
- In triangle ABC, we can use the tangent of angle ABC:
tan(angle)=oppositeadjacent
- Here, the opposite side is AC (20 m) and the adjacent side is BC.
- Therefore, we have:
tan(60∘)=ACBC=20BC
5. Substitute the Value of Tan 60 Degrees:
- We know that:
tan(60∘)=√3
- Substituting this into the equation gives:
√3=20BC
6. Rearrange to Solve for BC:
- Rearranging the equation to find BC:
BC=20√3
7. Rationalize the Denominator:
- To express BC in a more standard form, we can rationalize the denominator:
BC=20√3⋅√3√3=20√33
8. Final Answer:
- The distance from point B to the foot of the tower C is:
BC=20√33 meters
- Draw a vertical line representing the tower AC.
- Mark point C at the base of the tower.
- Mark point B on the ground such that angle ABC is 60 degrees.
- The height AC = 20 m.
- Triangle ABC is a right triangle where:
- AC (height of the tower) = 20 m
- Angle ABC = 60 degrees
- BC (distance from point B to the foot of the tower) is what we need to find.
- In triangle ABC, we can use the tangent of angle ABC:
tan(angle)=oppositeadjacent
- Here, the opposite side is AC (20 m) and the adjacent side is BC.
- Therefore, we have:
tan(60∘)=ACBC=20BC
- We know that:
tan(60∘)=√3
- Substituting this into the equation gives:
√3=20BC
- Rearranging the equation to find BC:
BC=20√3
- To express BC in a more standard form, we can rationalize the denominator:
BC=20√3⋅√3√3=20√33
- The distance from point B to the foot of the tower C is:
BC=20√33 meters
Similar Questions
In the figure-2, the angle of elevation of the top of tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m. find the distance of the point from the foot of the tower.
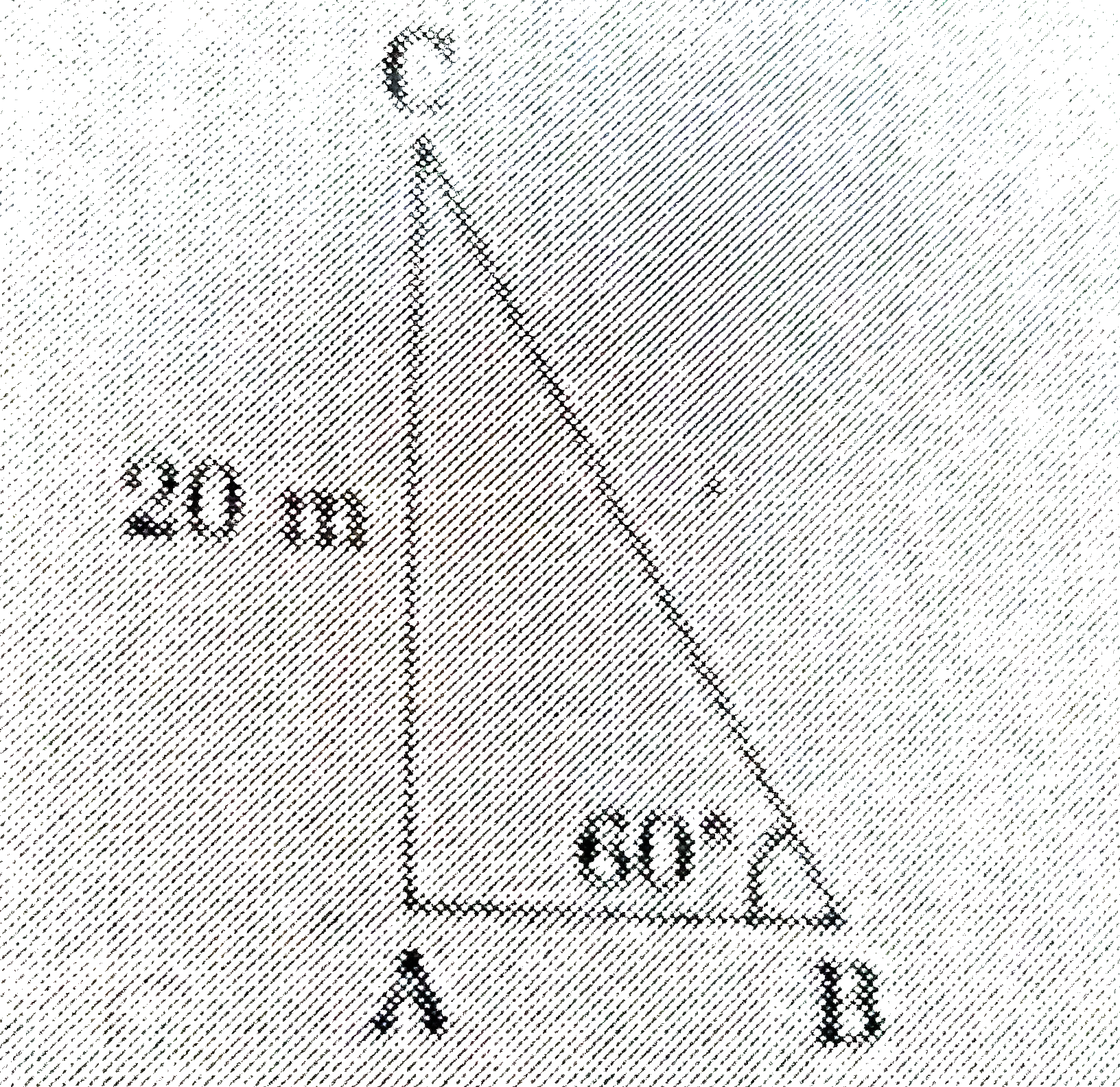
View SolutionIn figure , the angle of elevation of the top of a tower AC from a point B on the ground is 60∘ . If the height of the tower is 20 m, Find the distance of the point from the foot of the power .
View SolutionThe angle of elevation of the top of a tower from a point 40 m away from its foot is 60∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower is 30∘ . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View Solution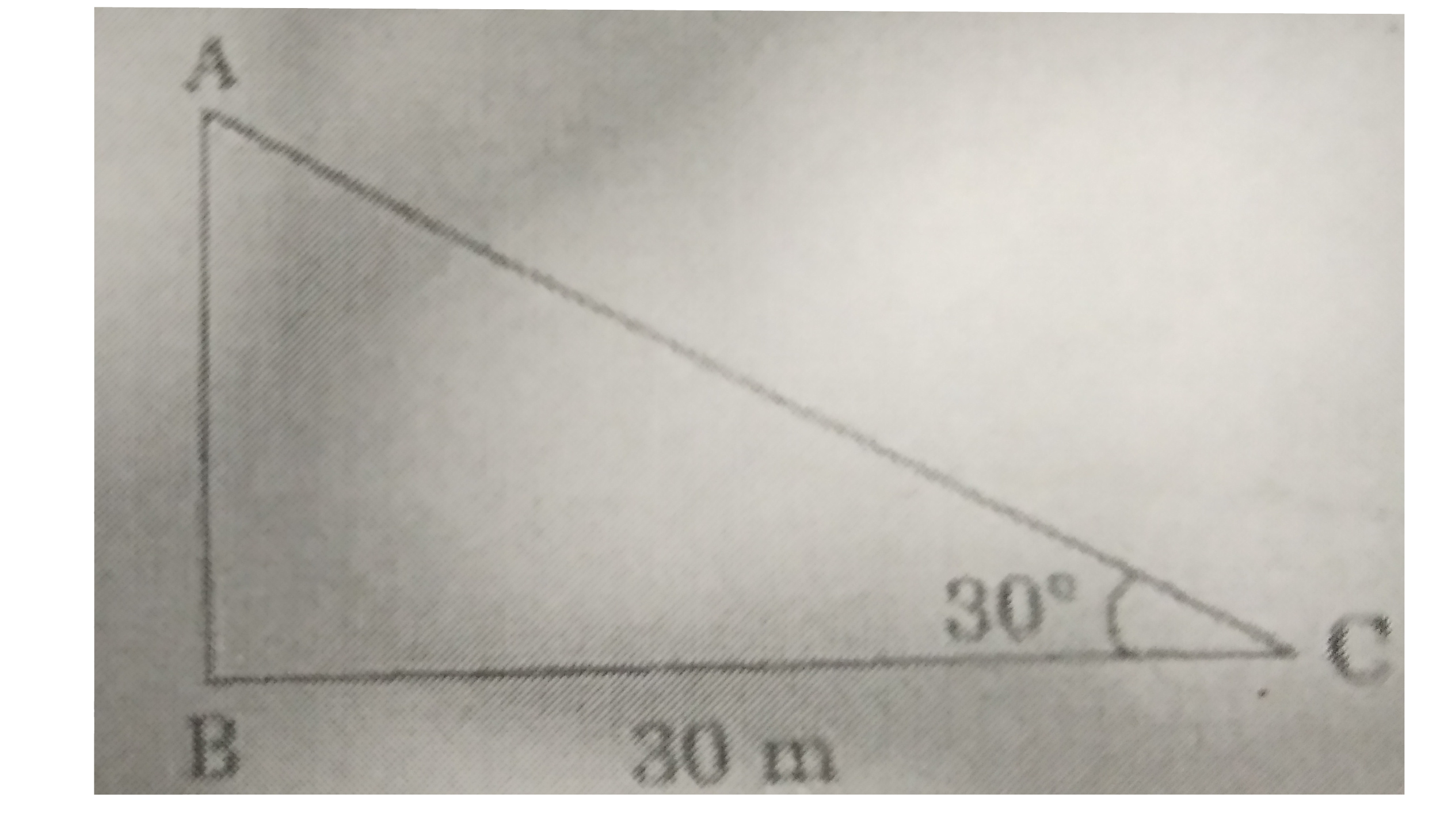
If figure, the angle of elevation of the top of a tower from a point C on the ground which is 30 m away from the foot of the tower, is 30∘. Find th height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 40 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground is 60∘. which is 25 m away from the foot of the tower. Find the height of the tower
View SolutionThe angle elevation of the top of a tower from a point C on the ground. Which is 30 m away from the foot of the tower is 30∘ . Find the height of the tower.

View Solution
