In Figure, time and distance graph of a linear motion is given. Two positions of time and distance are recorded as, when T = 0, D = 2 and when T = 3, D = 8. Using die concept of slope, find law of motion, i.e., how distance depends upon time.
To find the law of motion, i.e., how distance (D) depends upon time (T), we will use the concept of slope from the given points on the graph.
1. Identify the Points:
We have two points from the problem:
- Point A: (T = 0, D = 2)
- Point B: (T = 3, D = 8)
2. Calculate the Slope:
The slope (m) of a line is given by the formula:
m=y2−y1x2−x1
Here, we can consider the points as:
- (x1,y1)=(0,2) (Point A)
- (x2,y2)=(3,8) (Point B)
Plugging in the values:
m=8−23−0=63=2
3. Form the Equation of the Line:
The slope-intercept form of a line is given by:
D=mT+b
where m is the slope and b is the y-intercept. We know m=2. To find b, we can use one of the points. Let's use Point A (0, 2):
2=2(0)+b⟹b=2
4. Write the Final Equation:
Now substituting m and b into the equation:
D=2T+2
Conclusion:
The law of motion, which describes how distance depends on time, is given by:
D=2T+2
We have two points from the problem:
- Point A: (T = 0, D = 2)
- Point B: (T = 3, D = 8)
The slope (m) of a line is given by the formula:
m=y2−y1x2−x1
Here, we can consider the points as:
- (x1,y1)=(0,2) (Point A)
- (x2,y2)=(3,8) (Point B)
m=8−23−0=63=2
The slope-intercept form of a line is given by:
D=mT+b
where m is the slope and b is the y-intercept. We know m=2. To find b, we can use one of the points. Let's use Point A (0, 2):
2=2(0)+b⟹b=2
Now substituting m and b into the equation:
D=2T+2
The law of motion, which describes how distance depends on time, is given by:
D=2T+2
Topper's Solved these Questions
- STRAIGHT LINESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - Exercise
207 Videos
- STATISTICSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - STATISTICSEXERCISE - MISCELLANEOUS EXERCISE
7 Videos
- TRIGNOMETRIC FUNCTIONSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE
10 Videos
Similar Questions
In figure, time and distance graph of a linear motion is given. Two positions of time and distance recorded and when T=0, D=2 and when T=3, D=8. Using the concept of slope, find law of motion i.e. how distance depends upon time.
View SolutionFigure given shows the distance - time graph of the motion of a car. It follows from the graph that the car is
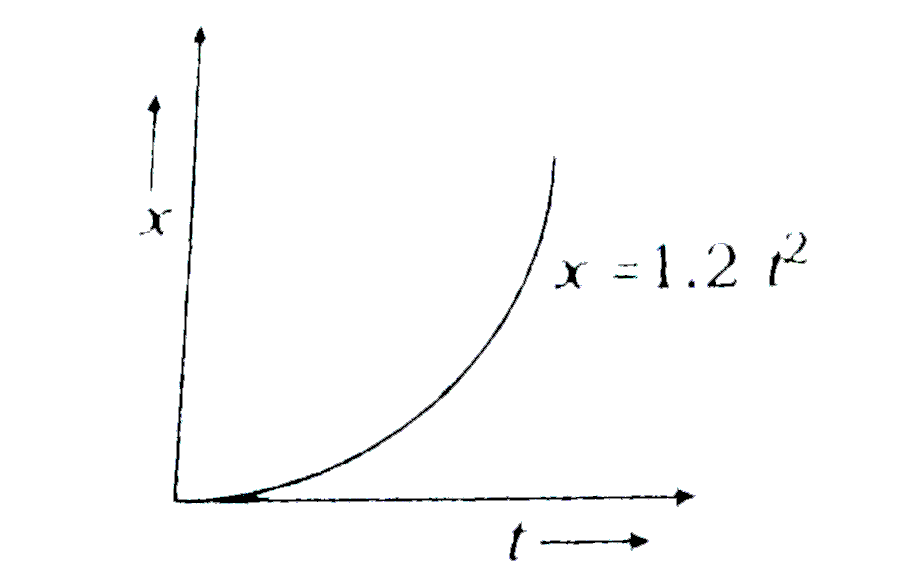
View Solution
Knowledge Check
The speed-time graph of a particle moving along a fixed direction as shown in the figure. The distance traversed by the particle between t = 0 s to t = 10 s is
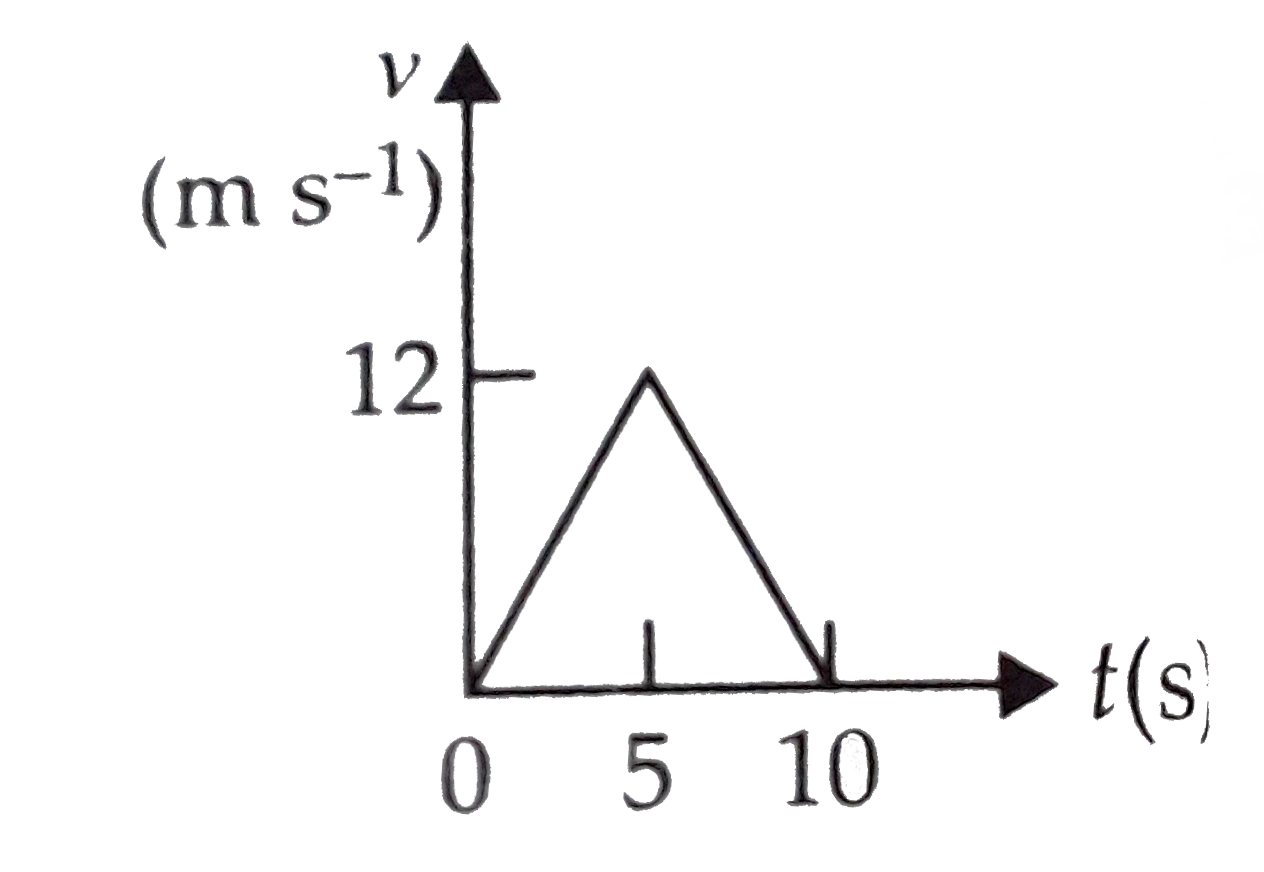 A20 mB40 mC60 mD80 m
A20 mB40 mC60 mD80 m
The velocity time graph of a linear motion is shown in the figure. The distance from the starting point after 8 seconds will be
 .
.
View SolutionAcceleration - time graph for a particle is given in figure. If it starts motion at t = 0, distance travelled in 3 s will be

View SolutionThe speed - time graph of a particle moving along a solid curve is shown below. The distance traversed by the particle from t = 0 to t = 3 is
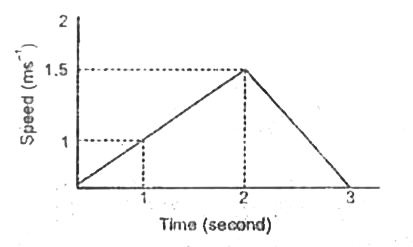
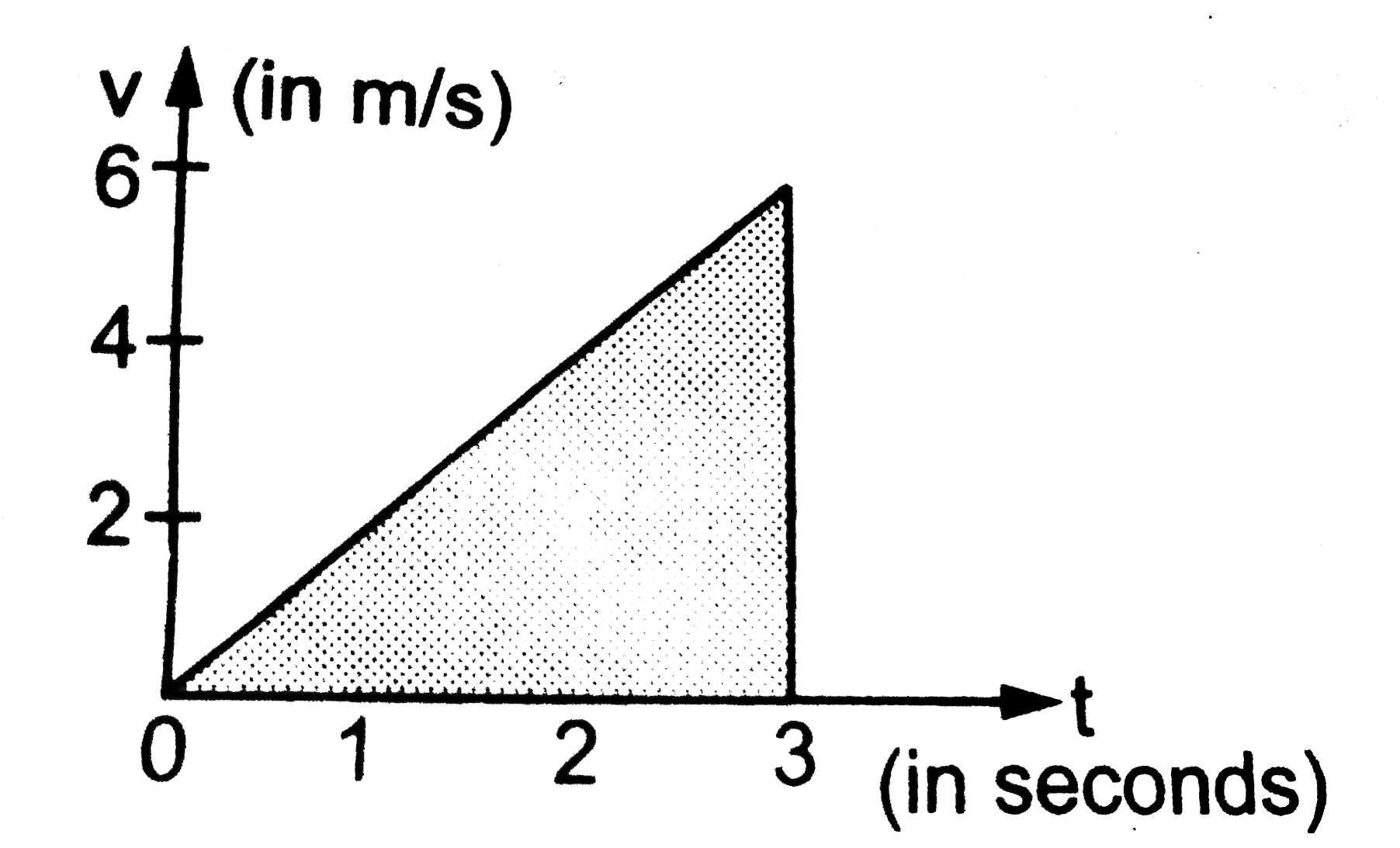
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
View SolutionThe displacement of a particle performing simple harmonic motion is given by, x=8sinωt + 6 cos ωt, where distance is in cm and time is in second. What is the amplitude of motion?
View SolutionPosition time graph is given find average speed in time t=0 and t=15sec is

View SolutionThe position-time graph of a body of mass 2 kg is as given in figure . What is the impulse on the body at t = 0 s and t = 4 s .
View Solution
