In figure, time and distance graph of a linear motion is given. Two positions of time and distance recorded and when T=0, D=2 and when T=3, D=8. Using the concept of slope, find law of motion i.e. how distance depends upon time.
To find the law of motion that describes how distance depends on time using the given points on the time-distance graph, we can follow these steps:
1. Identify the Given Points:
We have two points from the problem:
- When T=0, D=2 (Point A: (0,2))
- When T=3, D=8 (Point B: (3,8))
2. Plot the Points:
On a graph, plot the points (0,2) and (3,8). Draw a straight line connecting these two points since the motion is linear.
3. Calculate the Slope (m):
The slope of the line can be calculated using the formula:
m=y2−y1x2−x1
Here, (x1,y1)=(0,2) and (x2,y2)=(3,8). Substituting these values:
m=8−23−0=63=2
4. Use the Point-Slope Form of the Line:
The equation of a line can be expressed in point-slope form:
D−D1=m(T−T1)
Using point (0,2):
D−2=2(T−0)
5. Rearrange the Equation:
Simplifying the equation gives:
D−2=2T
Adding 2 to both sides:
D=2T+2
6. Conclusion:
The law of motion that describes how distance depends on time is:
D=2T+2
We have two points from the problem:
- When T=0, D=2 (Point A: (0,2))
- When T=3, D=8 (Point B: (3,8))
On a graph, plot the points (0,2) and (3,8). Draw a straight line connecting these two points since the motion is linear.
The slope of the line can be calculated using the formula:
m=y2−y1x2−x1
Here, (x1,y1)=(0,2) and (x2,y2)=(3,8). Substituting these values:
m=8−23−0=63=2
The equation of a line can be expressed in point-slope form:
D−D1=m(T−T1)
Using point (0,2):
D−2=2(T−0)
Simplifying the equation gives:
D−2=2T
Adding 2 to both sides:
D=2T+2
The law of motion that describes how distance depends on time is:
D=2T+2
Topper's Solved these Questions
Similar Questions
In the following figure, the time-distance graph is shown for a linear motion. As time T=0, distance is 2 units and at T=3, distance =8 units. Using slopes, find the relation between distance and time.
View SolutionIn Figure, time and distance graph of a linear motion is given. Two positions of time and distance are recorded as, when T = 0, D = 2 and when T = 3, D = 8. Using die concept of slope, find law of motion, i.e., how distance depends upon time.
View SolutionThe velocity time graph of a linear motion is shown in the figure. The distance from the starting point after 8 seconds will be
 .
.
View SolutionAcceleration - time graph for a particle is given in figure. If it starts motion at t = 0, distance travelled in 3 s will be

View SolutionThe displacement of a particle performing simple harmonic motion is given by, x=8sinωt + 6 cos ωt, where distance is in cm and time is in second. What is the amplitude of motion?
View SolutionThe distance s of a particle in time t is given by s=t3−6t2−4t−8. Its acceleration vanishes at t=
View SolutionFind the distance between the points A(2,3,1)and B(−1, 2, −3) , using vector method.
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
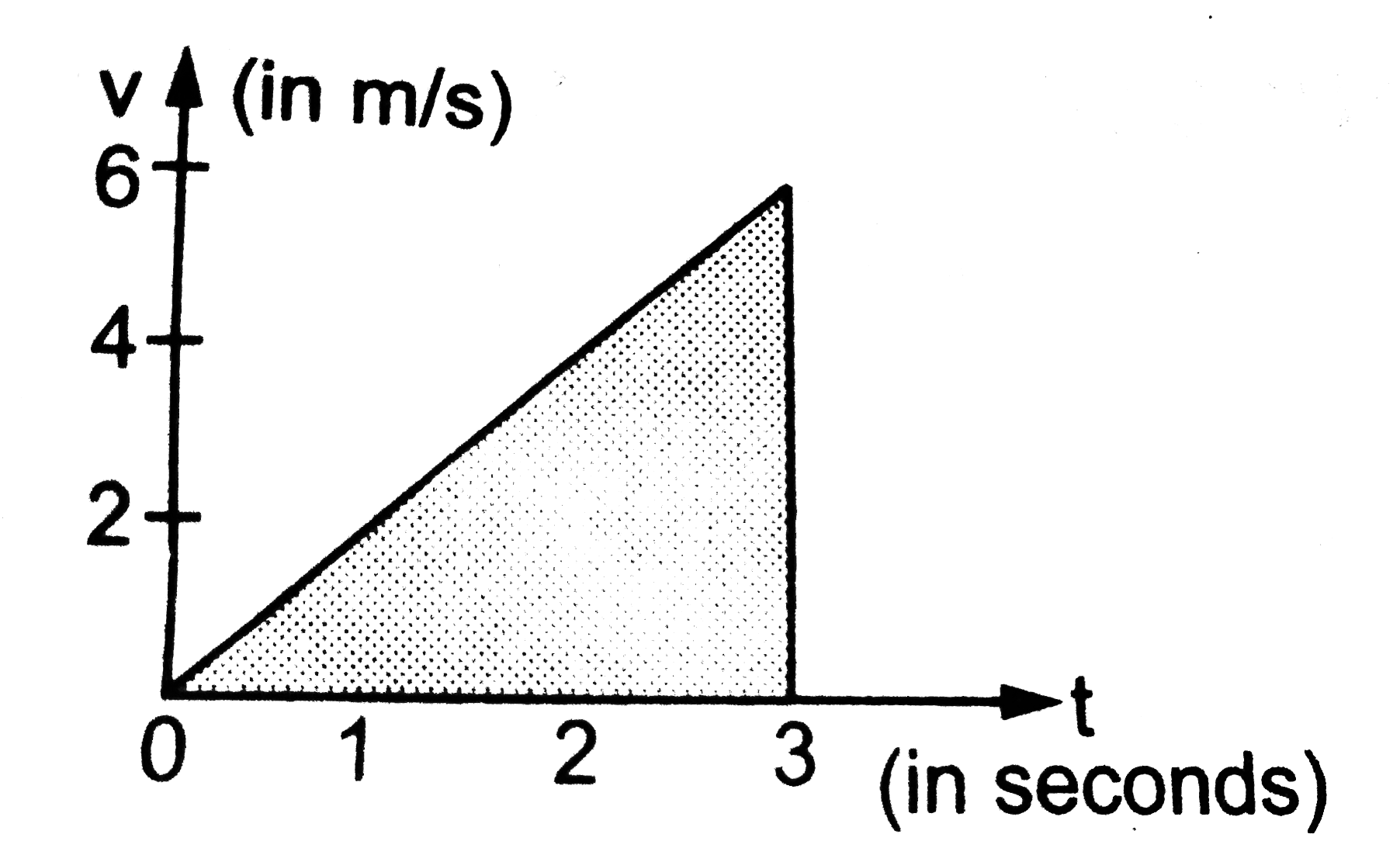
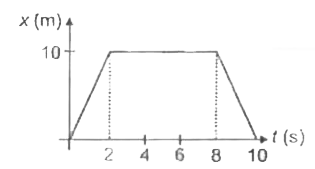
View SolutionThe position - time graph for a particle moving along a straight line is shown in figure. The total distance travelled by it in time t = 0 to t = 10 s is
View SolutionIn the graph represent direction of distance (d) vs time (t) ?
View Solution
