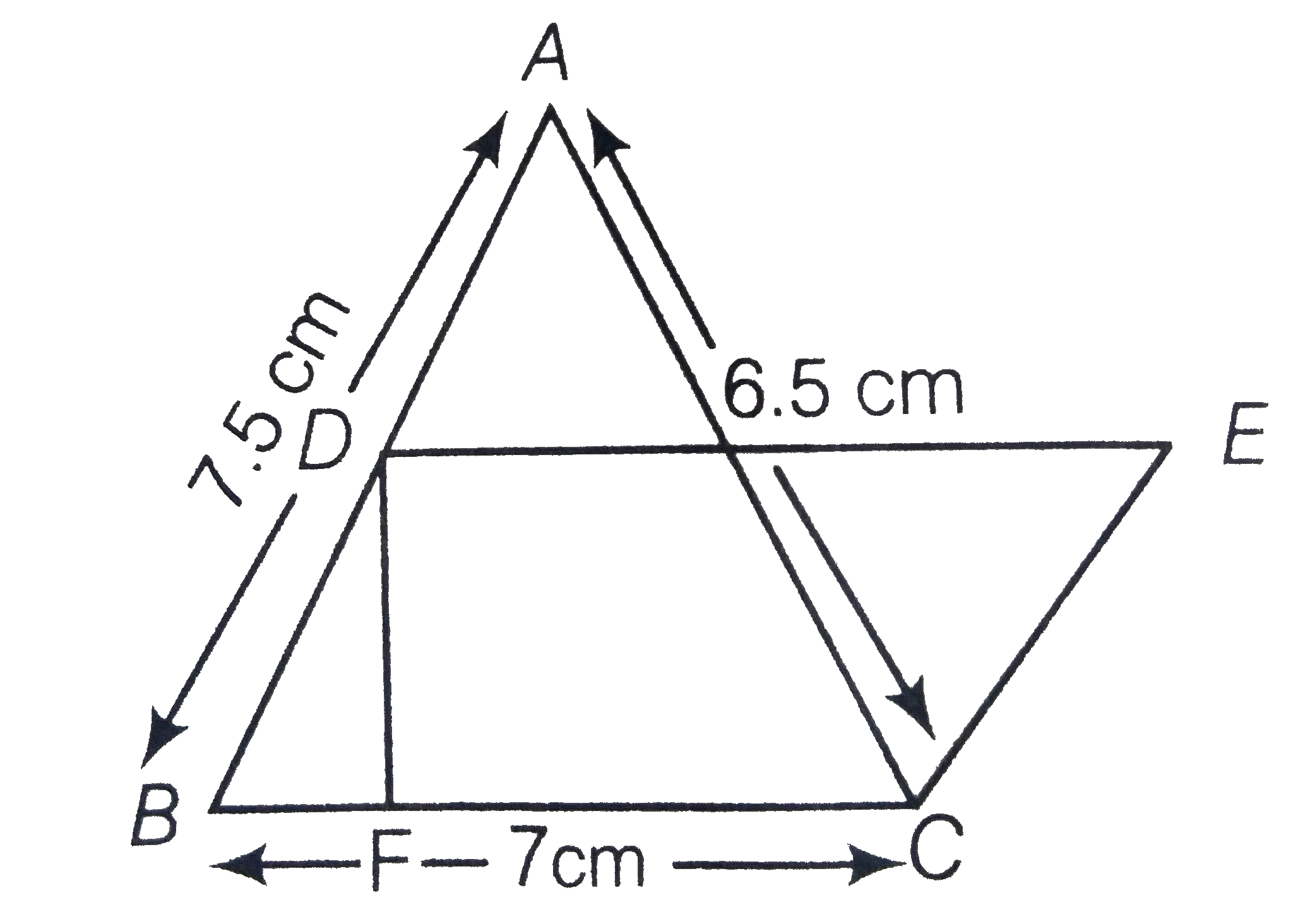
In figure, $△ A B C$ has sides $A B = 7.5 c m, A C = 6.5 c m$ and $B C = 7 c m .$ On base $B C$ a parallelogram $D B C E$ of same area as that of $△ A B C$ is constructed. Find the height $D F$ of the parallelogram.

A

$3 cm$

B

$7 cm$

C

$5 cm$

D

$6 cm$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Sides of triangle $A B C$ are $7.5 c m, 7 c m$ and $6.5 c m .$
the semi-perimeter of $Δ A B C$ ,
$s = \frac{7.5 + 7 + 6.5}{2} = \frac{21}{2} = 10.5 c m$
Area of $Δ = \sqrt{s (s - a) (s - b) (s - c)}$
$= \sqrt{10.5 (10.5 - 7.5) (10.5 - 7) (10.5 - 6.5)}$
$= \sqrt{10.5 \times 3 \times 3.5 \times 4} = \sqrt{31.5 \times 14}$
$= \sqrt{441} = 21 c m^{2}$
Now, as on base $B C$ a parallelogram $D B C E$ of same area as that of $Δ A B C$ is constructed.
Therefore, area of parallelogram DBCE = 21 $c m^{2}$ . Also, area of parallelogram $Δ B C E = B C \times D F$ .
$∴ B C \times D F = 12 c m^{2}$
$\Rightarrow 7 \times D F = 21 c m^{2}$
$\Rightarrow D F = 21 c m^{2} \div 7 c m = 3 c m$
Hence, the height $D F$ of the parallelogram $= 3 c m .$

|

Updated on:21/07/2023

Class 9 MATHS HERONS FORMULA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
In figure , $D E || B C$ in triangle ABC such that BC = 8 cm , AB = 6 cm and DA = 1.5 cm .find DE.

A2 cm
B3 cm
C4 cm
D5 cm
Question 2 - Select One
In $Δ A B C$ , $A B = 6 \sqrt{3} c m$ , $A C = 12 c m$ and $B C = 6 c m$ . Then $∠ B$ is
A $45^{\circ}$
B $60^{\circ}$
C $90^{\circ}$
D $120^{\circ}$
Question 3 - Select One
In a triangle ABC if sides AB = c = 4 cm, side AC = b = 6 cm and BC = a = 7, then answer the following questions
The length of median AD is
A $\frac{53}{2}$ cm
B $\frac{1}{2} \sqrt{55}$ cm
C $\sqrt{\frac{53}{2}}$ cm
D $\sqrt{\frac{63}{2}}$ cm

NAGEEN PRAKASHAN-HERONS'S FORMULA-Problems From NCERT / Exemplar

Home
Ask Doubt
Profile