A circle is inscribed in △ABC having sides AB=8cm, BC=7cm and AC=5cm. Find AD, BE and CF.
Step by step video & image solution for A circle is inscribed in triangleABC having sides AB=8 cm, BC=7 cm and AC=5 cm. Find AD, BE and CF. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
A circle is inscribed in Δ PQR having sides 8 cm, 10 cm and 12 cm. A circle touches the sides PQ, QR and RP at D, E and F. Find PD
A5 cmB6 cmC4 cmD10 cmA circle is inscribed in a triangle ABC. It touches the sides AB, BC and AC at the points R, P and Q respectively. If AQ = 4.5 cm, PC = 5.5 cm and BR = 6 cm, then the perimeter of the triangle ABC is:
एक वृत्त किसी त्रिभुज ABC में अन्तर्निहित है | यह भुजाओं AB, BC और AC को क्रमशः बिंदु R, P और Q पर स्पर्श करता है | यदि AQ = 4.5 सेमी, PC = 5.5 सेमी और BR = 6 सेमी है, तो त्रिभुज ABC का परिमाप ज्ञात करें |A30.5cm.B28cm.C32cm.D26.5cm.The sides AB, BC and AC of a ΔABC are 12 cm, 8 cm and 10 cm respectively. A circle is inscribed in the triangle touching AB, BC and AC at D, E and F, respectively. The difference between the lengths of AD and CE is:
Aa)4 cmBb)5 cmCc)3 cmDd)2cm
A circle is inscribed in a △ABC having sides 8 cm, 10 cm and 12 cm as shown in figure. Find AD, BE and CF.
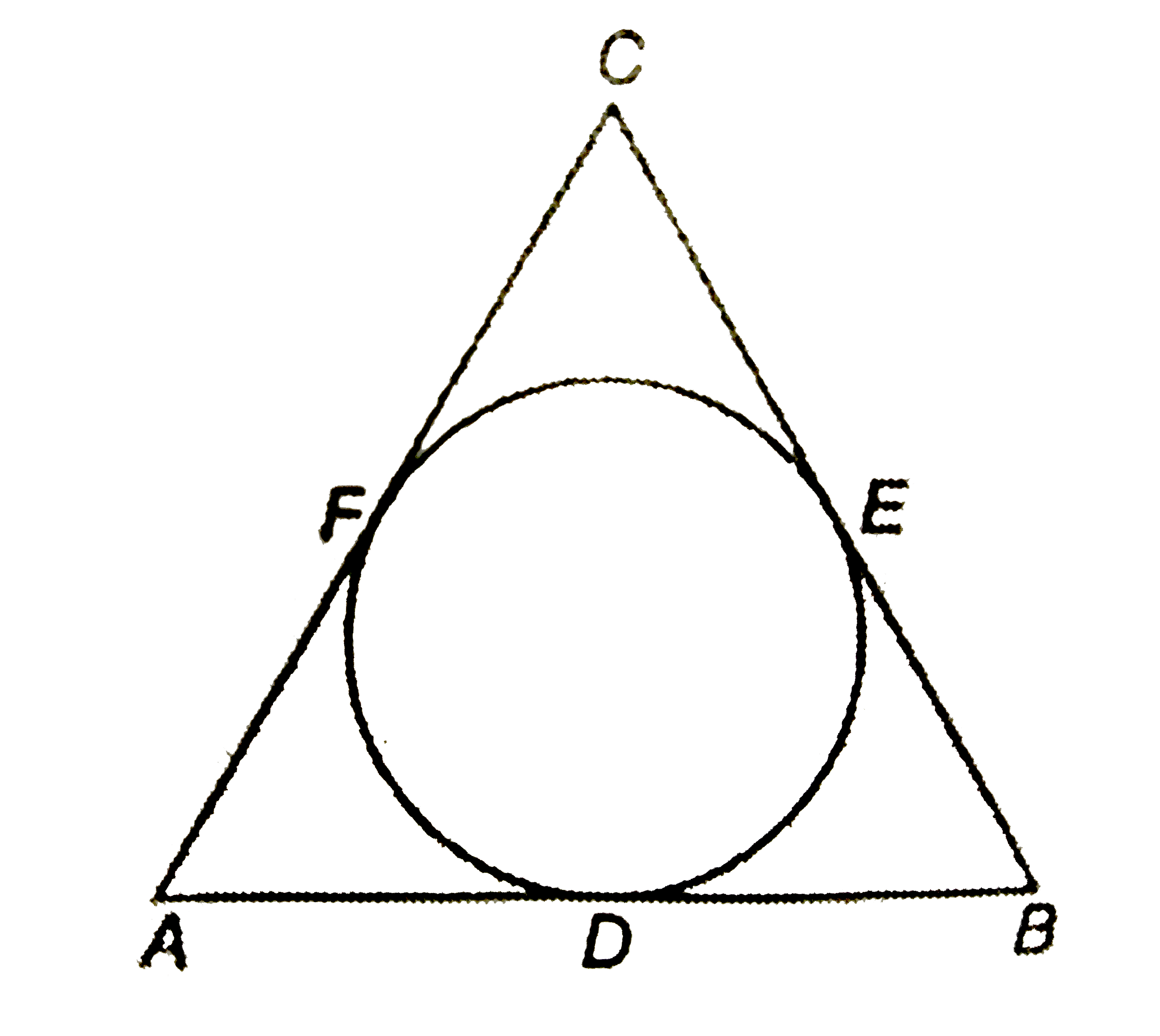
View SolutionA circle in inscribed in a ΔABC having sides 8 cm , 10 cm and 12 cm in Fig Find AD, BE and CF.
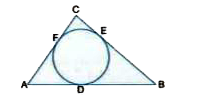
View SolutionIn the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View SolutionIn the given figure, a circle inscribed in a triangle ABC, touches the sides AB, BC and AC at points D, E and F respectively. If AB= 12 cm, BC= 8 cm and AC = 10 cm, find the lengths of AD, BE and CF.
View SolutionIn the given figure, a circle inscribed in a triangle ABC touches the sides AB, BC and CA at points D, E and F respectively. If AB = 14 cm, BC = 8 cm and CA = 12 cm. Find the lengths AD, BE and CF.
View Solution
