In Figure, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and c
The correct Answer is:=48∘
Step by step video, text & image solution for In Figure, two straight lines P Q\ a n d\ R S intersect each other at Odot If /_P O T=75^0, find the values of a , b\ a n d\ c by Maths experts to help you in doubts & scoring excellent marks in Class 7 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINES AND ANGLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINES AND ANGLES EXERCISE - QUESTIONS BANK
22 Videos
- LINES AND ANGLES BOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINES AND ANGLES EXERCISE - SELF ASSESSMENT SHEET
10 Videos
- LINEAR EQUATIONS IN ONE VARIABLEBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - LINEAR EQUATIONS IN ONE VARIABLEEXERCISE - Unit Test -2
20 Videos
- NUMBERSBOOK - S CHAND IIT JEE FOUNDATIONCHAPTER - NUMBERSEXERCISE - SELF ASSESSMENT SHEET-1
10 Videos
Similar Questions
In Figure, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and c
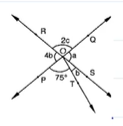
View SolutionIn Fig. 12, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and ⋅
View SolutionIn Figure, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and c
View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

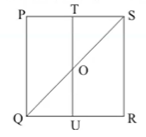
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
View SolutionTwo circles intersect each other at the points P and Q. Two straight lines through P and Q intersect one circle at the points A and C and the other circle at B and D. Prove the AC|| BD
View SolutionIn Figure, two chords AB and CD intersect each other at the point P. Prove that:
(i) ΔAPC~ΔDPB
(ii) AP⋅PB=CP⋅DP
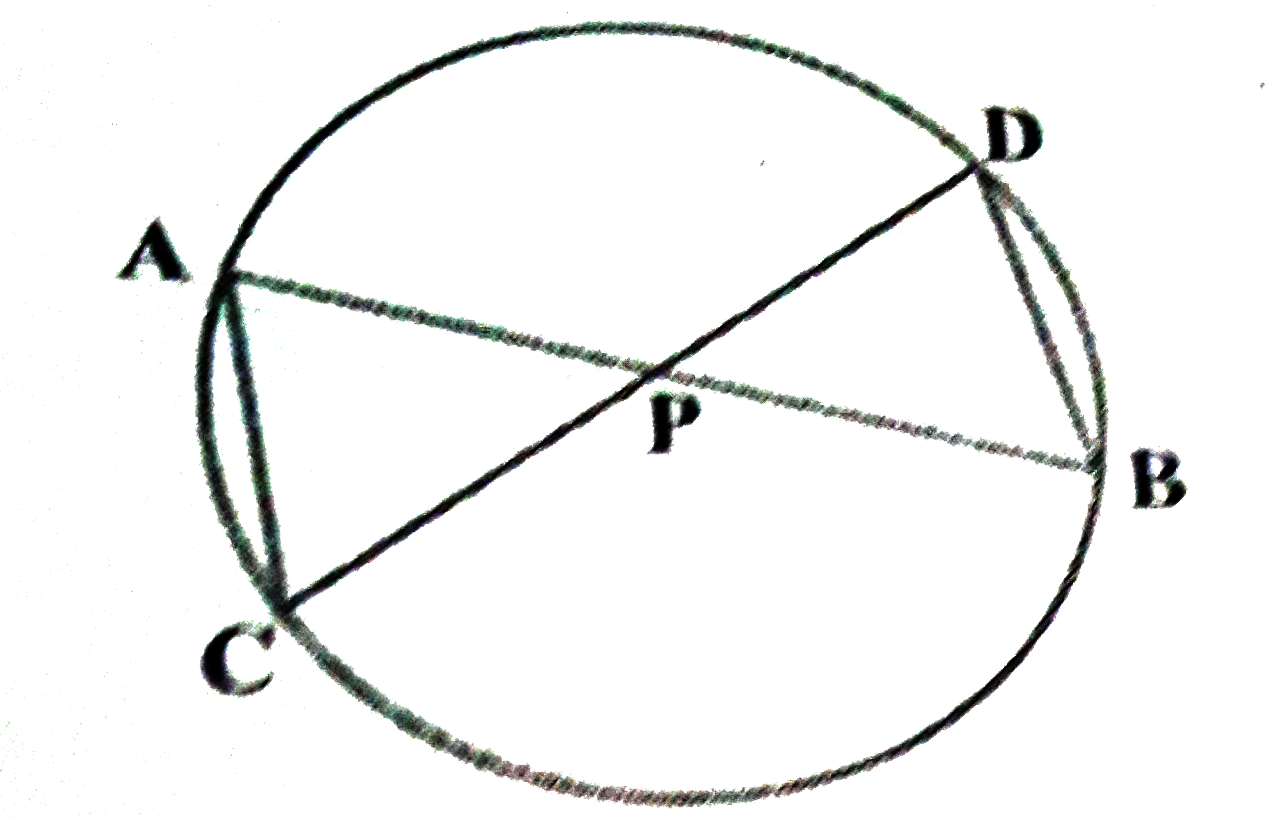
View SolutionABCD is a parallelogram. P is the mid-point of AB.BD and CP intersect at Q such that CQ:QP=3:1. If ar (PBQ)=10 cm2, find the area of parallelogram ABCD
View Solution
