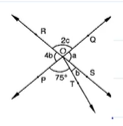
In Fig. 12, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and ⋅
To solve the problem step by step, we will use the properties of vertically opposite angles and linear pairs of angles.
1. Identify the Given Information:
- We have two intersecting lines PQ and RS at point O.
- The angle ∠POT=75∘.
2. Use the Property of Vertically Opposite Angles:
- Since ∠POT and ∠POS are vertically opposite angles, we can state:
∠POS=∠POT=75∘
3. Set Up the Equation for Linear Pair:
- The angles ∠POT, ∠A (which is ∠QOS), and ∠B (which is ∠POQ) form a linear pair. Therefore:
∠POT+∠A+∠B=180∘
- Substituting the known value:
75∘+A+B=180∘
- Rearranging gives:
A+B=180∘−75∘=105∘(Equation 1)
4. Relate Angles A, B, and C:
- From the problem, we know that:
A=4B(Equation 2)
- Also, since ∠B and ∠C are also vertically opposite angles, we have:
B=2C(Equation 3)
5. Substitute Equation 2 into Equation 1:
- Substitute A=4B into Equation 1:
4B+B=105∘
- This simplifies to:
5B=105∘
- Thus, solving for B:
B=105∘5=21∘
6. Find Angle A:
- Substitute B=21∘ back into Equation 2:
A=4B=4×21∘=84∘
7. Find Angle C:
- Substitute B=21∘ into Equation 3:
B=2C⟹21∘=2C
- Solving for C:
C=21∘2=10.5∘
Final Values:
- A=84∘
- B=21∘
- C=10.5∘
- We have two intersecting lines PQ and RS at point O.
- The angle ∠POT=75∘.
- Since ∠POT and ∠POS are vertically opposite angles, we can state:
∠POS=∠POT=75∘
- The angles ∠POT, ∠A (which is ∠QOS), and ∠B (which is ∠POQ) form a linear pair. Therefore:
∠POT+∠A+∠B=180∘
- Substituting the known value:
75∘+A+B=180∘
- Rearranging gives:
A+B=180∘−75∘=105∘(Equation 1)
- From the problem, we know that:
A=4B(Equation 2)
- Also, since ∠B and ∠C are also vertically opposite angles, we have:
B=2C(Equation 3)
- Substitute A=4B into Equation 1:
4B+B=105∘
- This simplifies to:
5B=105∘
- Thus, solving for B:
B=105∘5=21∘
- Substitute B=21∘ back into Equation 2:
A=4B=4×21∘=84∘
- Substitute B=21∘ into Equation 3:
B=2C⟹21∘=2C
- Solving for C:
C=21∘2=10.5∘
- A=84∘
- B=21∘
- C=10.5∘
Topper's Solved these Questions
Similar Questions
In Figure, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and c
View SolutionIn Fig. 12, two straight lines PQ and RS intersect each other at O. If ∠POT=750, find the values of a,b and ⋅
View SolutionIn Fig.79, DEBC. Find the value of x and y.
View SolutionIn Fig. 6.42, if lines PQ and RS intersect at point T, such that ∠PRT=40∘,∠RPT=95∘ and ∠TSQ=75∘, find ∠SQT.

View SolutionIn a quadrilateral ABCD, bisectors of angles A and B intersect at O such that ∠AOB=75∘, then write the value of ∠C+ ∠D
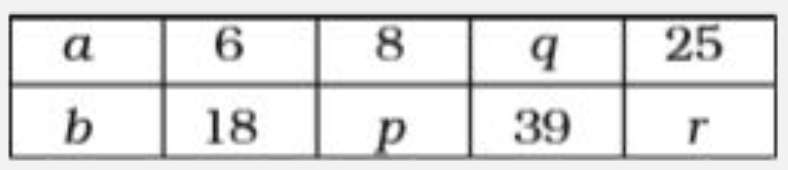
View SolutionIf a and b vary inversely to each other, then find the values of p, q, r .
View SolutionPQRS is a square such that PR and SQ intersect at O. State the measure of ∠POQ
View SolutionIn Fig. 63, line l ∣∣ m and a transversal n cuts them at P and Q respectively. If ∠1=750, find all other angles.
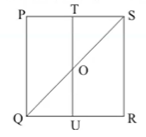
View SolutionIn Figure, PQRS is a square and T and U are, respectively, the mid-points of PS and QR . Find the area of OTS if PQ=8 cm.
View SolutionIn Fig. 64, AB∣∣CD and a transversal PQ cuts them at L and M respectively. If ∠QMD=1000, find all other angles.
View Solution
