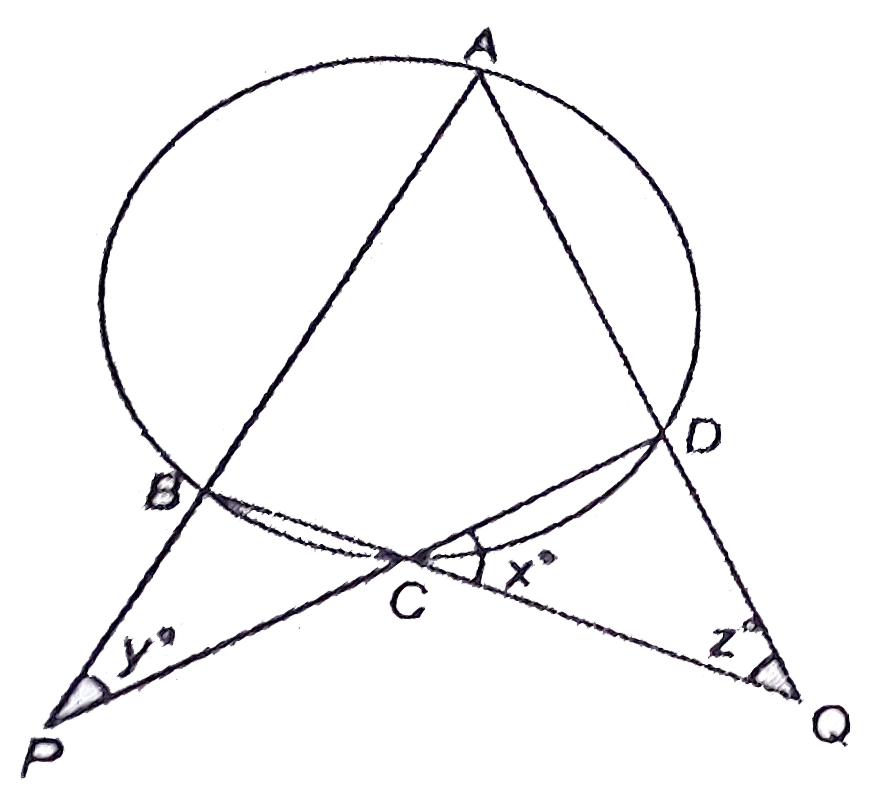
In given fig., if $\frac{x}{3} = \frac{y}{4} = \frac{z}{5}$ , then calculate the values of x,y and z.

Video Solution

Text Solution

Verified by Experts

In the figure, $\frac{x}{3} = \frac{y}{4} = \frac{z}{5} = k$ (say)
$\Rightarrow x = 3 k$
$y = 4 k$
and $z = 5 k$
In cyclic qudarilateral ABCD, the side BC is produced to Q.
$∴ ∠ A = ∠ D C Q = x$ ( $∵$ exterior angle of a cyclic quadrilateral is equal to its interior opposite angle)
Also, in $Δ C D Q$ , the side QD is produced to A
$\Rightarrow ∠ A D P = x + z$ ( $∵$ exterior angle of a triangle is equal to the sum of its two int., opposite angles)
Now, in $Δ A D P$ ,
$∠ A + ∠ A D P + ∠ A P D = 180^{\circ}$ ( $∵$ sum of angles of a triangle is $180^{\circ}$ )
$∴ x + (x = z) + y = 180^{\circ}$
$\Rightarrow 2 x + y + z = 180^{\circ}$
$\Rightarrow 2 (3 k) + 4 k + 5 k = 180^{\circ}$
$\Rightarrow 6 k + 4 k + 5 k = 180^{\circ}$
$\Rightarrow 15 k = 180^{\circ} \Rightarrow k = 180^{\circ} \div 15 = 12^{\circ}$
$∴ x = 3 k = 3 \times 12 = 36^{\circ}$
$y = 4 k = 4 \times 12 = 48^{\circ}$
and $z = 5 k = 5 \times 12 = 60^{\circ}$

|

Class 9 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $x = 10^{1.4}, y = 10^{0.7}, and$ x^(z) = y^(3), then what is the value of z?
A $0.5$
B $0.66$
C $1.5$
D $2$

NAGEEN PRAKASHAN ENGLISH-CIRCLE -Revision Exercise (long Answer Questions )

Home
Ask Doubt
Profile