In given figure, ABC is a triangle produced meets the circumcircle of ΔABC at Q, prove that CP=CQ
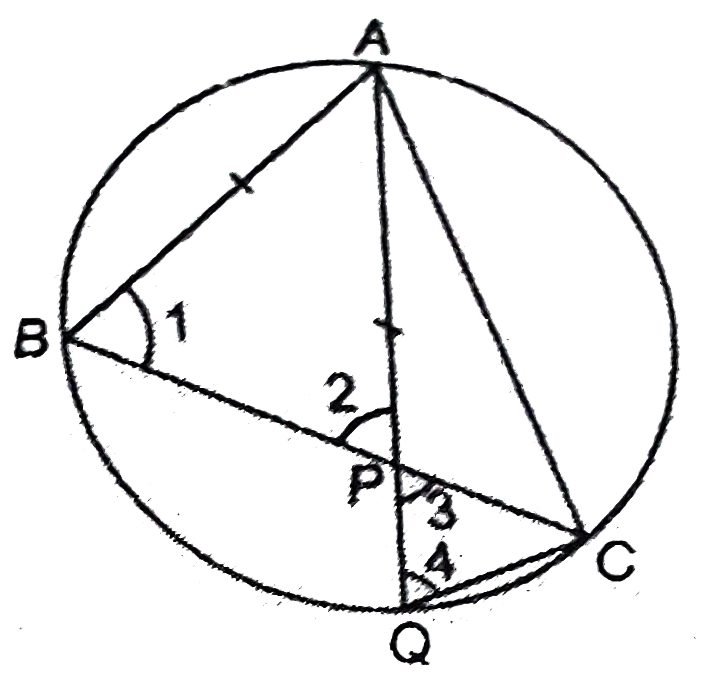
In ΔABP,
AB=AP (given)
∠1=∠2 (angles opposite to equal sides ) .......(1)
But ∠2=∠3 (vertically opposite angle) ......(2)
⇒∠1=∠3 [From (1) and (2)] .........(3)
But ∠1=∠4 (angles of same segment) .........(4)
∴∠3=∠4 [from (3)and (4)]
⇒CP=CQ (side opposite to equal of ΔCPQ)
Topper's Solved these Questions
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10a
22 Videos
- CIRCLE BOOK - NAGEEN PRAKASHANCHAPTER - CIRCLE EXERCISE - Exercise 10b
19 Videos
- AREA OF PARALLELOGRAMS AND TRIANGLESBOOK - NAGEEN PRAKASHANCHAPTER - AREA OF PARALLELOGRAMS AND TRIANGLESEXERCISE - Revision Exercise (long Answer Question)
5 Videos
- CO-ORDINATE GEOMETRY BOOK - NAGEEN PRAKASHANCHAPTER - CO-ORDINATE GEOMETRY EXERCISE - Exercise
8 Videos
Similar Questions
Let ABC be an acute angled triangle whose orthocentre is at H. If altitude from A is produced to meet the circumcircle of triangle ABC at D , then prove HD=4RcosBcosC
View SolutionI is the incentre of △ABC AI when produced meets the circumcircle of △ABC in D.If ∠BAC=66∘ and ∠ACB=80∘ Calculate (i) ∠DBC (ii) ∠IBC (iii) ∠BID
View Solution
Knowledge Check
I and O are incentre and circumcentre of a ΔABC. AI is produced and it intersects the circumcircle at D. ∠ABC=x,∠BID=y&∠BOD=z. Find z+xy
A3B1C2D4If R is the radius of the circumcircle of the ΔABCandΔ is its area then
AR=a+b+c2BR=a+b+cΔCR=abc4ΔDR=abcΔIn a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E , then find AB .AC+DE. AE.
A2AEBAE2C2AE2D3AE2
In the given figure, ABC is an equilateral triangle; PQ∣∣AC and AC is produced to R such that CR=BP. Prove that QR bisects PC
View SolutionIn the given figure, ABC is an equilibrium triangle, PQ||AC and AC is produced to R such that CR=BP. Prove that QR bisects PC.

View SolutionIn a triangle ABC, angle bisector of ∠BAC cut the side BC at D and meet the circumcircle of ΔABC at E. If AC = 4 cm, AD = 5 cm, DE = 3 cm. Find the length of AB.
View SolutionIn the givne figure, ABC is an equilateral triangle, PQ||AC and AC is produced to R such that CR = BP. Prove that QR bisects PC.

View SolutionIn the figure, ABC is a triangle. Measure of ΔABD, (in degrees) is
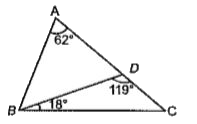
View Solution
