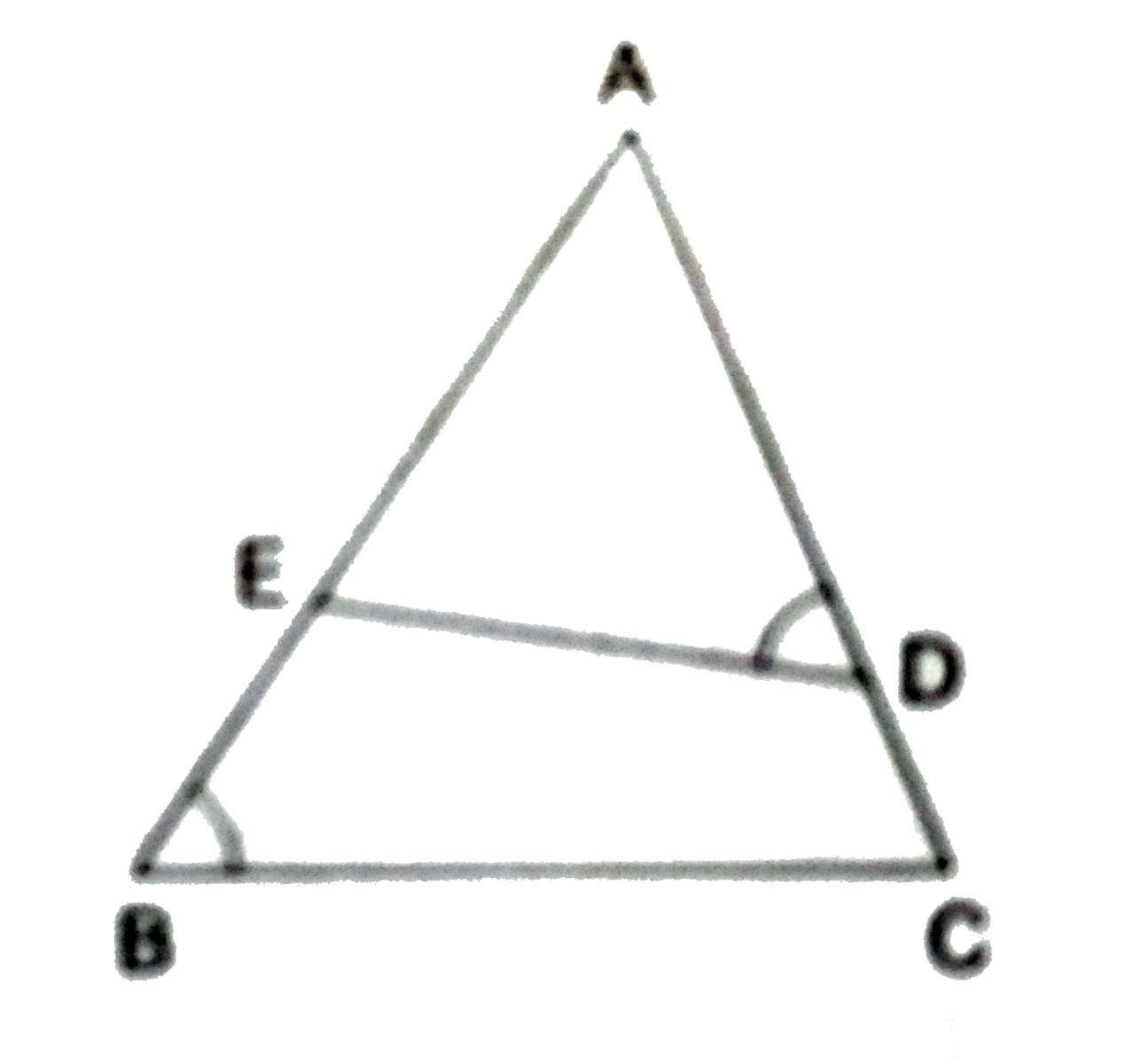
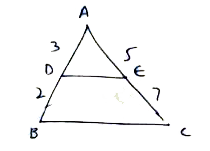
In that figure, if ΔABE≅ΔACD, show that ΔADE≅ΔABC.
Video Solution
Text Solution
ΔABE≅ΔACD (give)
∴AE=AD ...(i) [cpct]
and AB=AC ...(ii) [ cpct]
In ΔADEandΔABC, we have
∠DEA=∠BAC (common)
and ADAB=AEAC [ using (i) and (ii)]
∴ΔADE~ΔABC[ by SAS-similarity]
|
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - SOLVED EXAMPLE
4 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - EXERCISE 7 A
1 Video
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
In the given figure ar (ΔABC)= ar (ΔADE). AC is the median of ΔADE. If ar (ACE) =14cm2 then ar (ΔABC) = ?
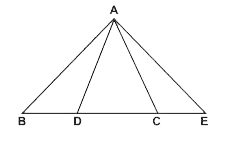 A14cm2B7cm2C21cm2D28cm2
A14cm2B7cm2C21cm2D28cm2If ΔABC~ΔPQR and 4A(ΔABC)=25A(ΔPQR) then AB : PQ = ?
A4:25B2:5C5:2D25:4In ΔABCand ΔDEF,AB=DEandBC=EF. Then one can infer that
ΔABC=ΔDEF, whenA∠BAC=∠EDFB∠ACB=∠EDFC∠ACB=∠DFED∠ABC=∠DEF
In figure ,D and E are Points on side BC of a ΔABC such that BD=CE and AD=AE.Show that ΔABD≅ΔACE.
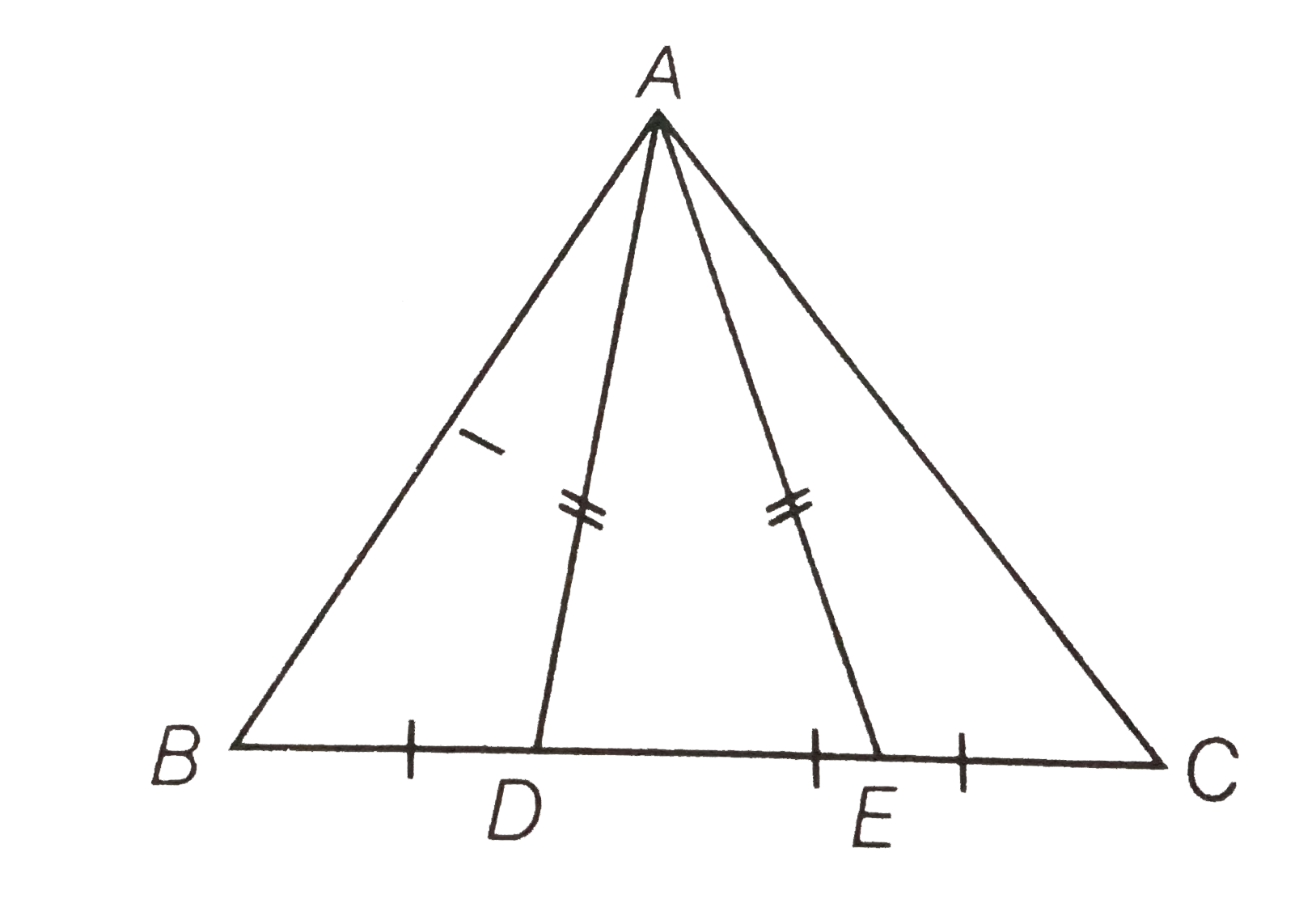
View SolutionIn the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).
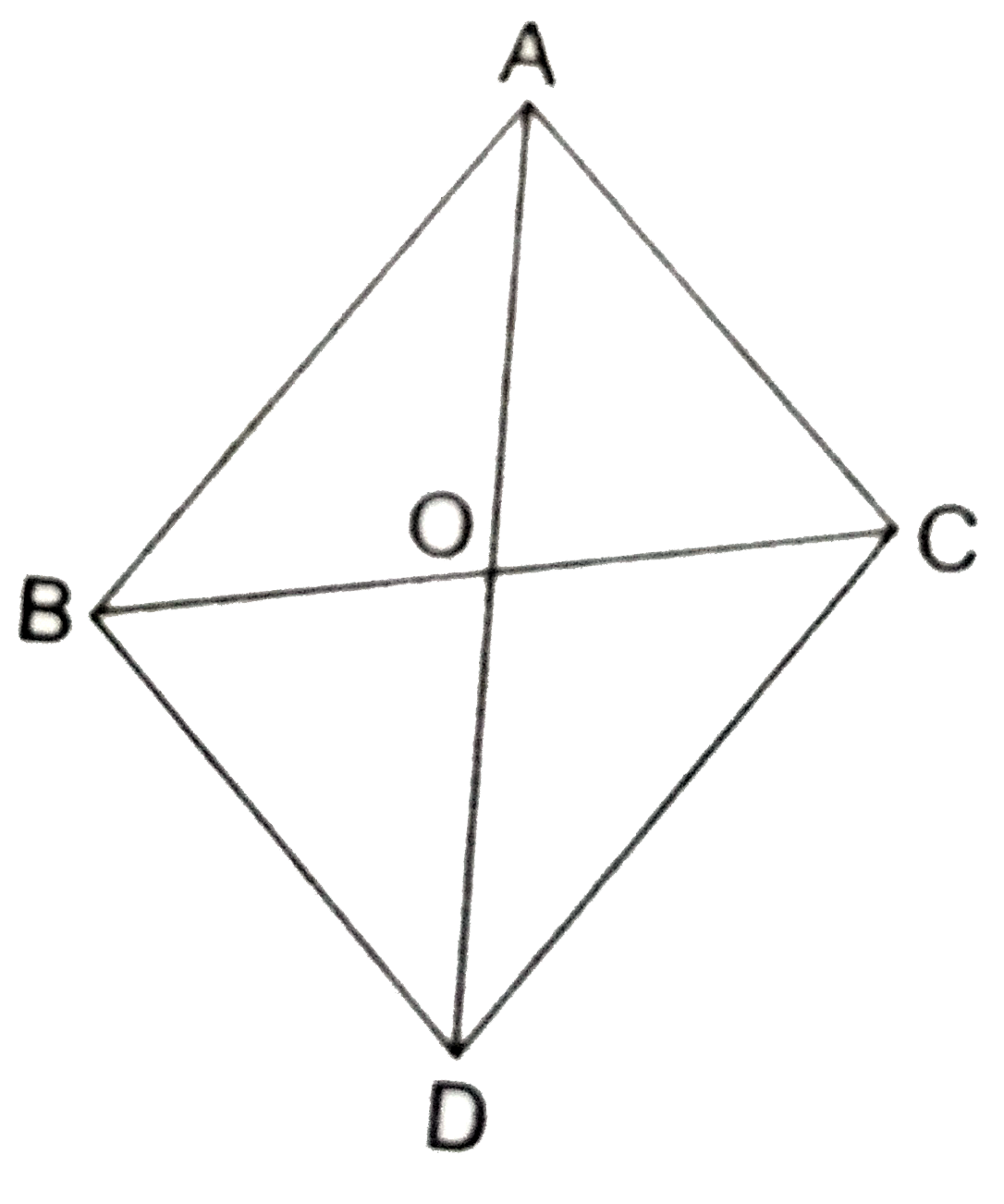
View SolutionIn the same figure, ΔABCandΔDBC are on the same base BC . If AD is intersects BC at O, prove that
ar(ΔABC)ar(ΔDBC)=AODO
View SolutionIn the adjoining figure, DE∣∣BC. Prove that area (ΔACD)= area (ΔABE)

View SolutionIn the given figure, ΔABCandΔDBC are on the same base BC. If AD intersects BC at O, prove that ar(ΔABC)ar(ΔDBC)=AODO
View Solution