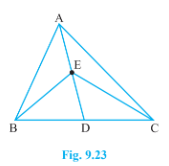
In the adjoining figure, E is a point on the median $A D$ of a $Δ A B C .$ Show that ar $(Δ A B E) = (Δ A C E) .$

Video Solution

|

Answer

Step by step video solution for In the adjoining figure, E is a point on the median AD of a DeltaABC. Show that ar (DeltaABE)=(DeltaACE). by Maths experts to help you in doubts & scoring excellent marks in Class 9 exams.

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Similar Questions

In the adjoining figure, E is a point on the median $A D$ of a $Δ A B C .$ Show that ar $(Δ A B E) = (Δ A C E) .$
View Solution
In Fig.9.23, E is any point on median AD of a $Δ A B C$ . Show that $a r (A B E) = a r (A C E) .$

View Solution
In the adjoining figure, P is the point in the interior of a parallelogram ABCD.Show that ar(DeltaAPB) ar(DeltaPCD) =1/2ar(||gm ABCD)
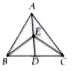
View Solution
In the figure, E is any point on median AD of a $△ A B C$ . Show that ar( $△ A B E$ )= ar( $△ A C E$ ).

View Solution
E is any point on median $A D$ of $∠ A B C$ .If $a r (Δ A B E) = 10 c m^{2}$ then $a r (Δ A C E)$ is
View Solution
In the adjoining figure, M is the midpoint of seg AB and seg CM is a median of $Δ A B C$ . Find $\frac{A (Δ A M C)}{A (Δ B M C)}$ .
View Solution
In the given figure, BE and CF are two equal altitudes of $Δ A B C$ .
Show that (i) $Δ A B E ≅ Δ A C F$ ,
(ii)AB = AC.

View Solution
In the adjoining figure, AD is the median of $Δ A B C$ and X be any point on side AD. Prove that:
area $(Δ A B X) = area (Δ A C X)$

View Solution
In the adjoining figure, AD is the median of $Δ A B C$ and X be any point on side AD. Prove that:
area $(Δ A B X) = area (Δ A C X)$

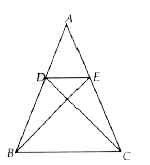
View Solution
In the figure ,if $Δ A B E ≅ Δ A C D$ , Show that $Δ A D E ~ Δ A B C$ .

View Solution

In the adjoining figure, E is a point on the median AD of a ΔABC. Show that ar (ΔABE)=(ΔACE).

Similar Questions

Recommended Questions

In the adjoining figure, E is a point on the median $A D$ of a $Δ A B C .$ Show that ar $(Δ A B E) = (Δ A C E) .$